Cách giải Các dạng toán Hình học lớp 5 điển hình gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết Các dạng toán Hình học lớp 5 điển hình. Bên cạnh có là 10 bài tập vận dụng để học sinh ôn luyện dạng Toán 5 này.
Bạn đang xem: Các bài toán cơ bản lớp 5 về hình học
Các dạng toán Hình học lớp 5 điển hình và cách giải
Giải các bài toán có yếu tố hình học
I/ Lý thuyết
Chuyên đề này sẽ giúp các em giải các bài toán có chứa yếu tố hình học trong đề bài.
II/ Các dạng bài tập
II.1/ Dạng 1: Các bài toán về các hình học phẳng
1. Phương pháp giải
Các bài toán về các hình học phẳng được chia ra làm 2 dạng nhỏ:
- Các bài toán không có nội dung thực tế: là các bài toán đề bài cho một hình vẽ, cho số liệu và yêu cầu tính diện tích, chu vi hoặc một cạnh nào đó...
- Các bài toán có chứa nội dung thực tế: Trong đề bài toán có những dữ liệu liên quan đến đời sống thực tế.
- Đối với dạng toán này chúng ta cần nhớ và áp dụng công thức tính chu vi, diện tích các hình học phẳng đã học: hình vuông, hình chữ nhật, hình tam giác, hình tròn, hình thang, hình bình hành..
2. Bài tập minh họa
Bài 1: Tính diện tích hình ngũ giác ABCDE có kích thước như hình vẽ.
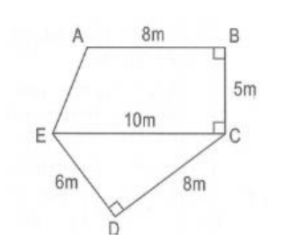
Hướng dẫn: Diện tích hình ngũ giác ABCDE bằng tổng diện tích hình thang ABCE và diện tích hình tam giác ECD.
Diện tích hình thang ABCE là: (8 + 10) x 5 : 2 = 45 (m2 )
Diện tích hình tam giác ECD là: 6 x 8 : 2 = 24 (m2 )
Diện tích hình ngũ giác ABCDE là: 45 + 24 = 69 (m2 )
Đáp số: 69m2 Bài 2: Một thửa ruộng hình thang có đáy lớn 120m, đáy bé bằng 23đáy lớn. Đáy bé dài hơn chiều cao 5m. Trung bình cứ 100m2 thì thu hoạch được 72kg thóc. Tính số ki-lô-gam thóc thu được trên thửa ruộng đó.
Hướng dẫn:
+Áp dụng cách tính tìm phân số của một số để tìm đáy bé.
+Tìm chiều cao dựa vào độ dài đáy bé.
+Tính diện tích thửa ruộng hình thang.
+Tính số thóc thu hoạch được
Đáy bé dài số ki-lô-mét là: 120×23=80(m)
Chiều cao là: 80 – 5 = 75 (m)
Diện tích thửa ruộng là:
(120 + 80) x 75 : 2 = 7500 (m2 )
Thửa ruộng đó thu hoạch được số ki-lô-gam thóc là:
7500 : 100 x 72 = 5400 (kg)
Đáp số: 5400 kg thóc
II.2/ Dạng 2: Các bài toán về các hình khối
1. Phương pháp giải
- Dạng toán này bao gồm những bài tập liên quan đến hình lập phương, hình hộp chữ nhật
- Để giải được các dạng toán này, các em cần nắm rõ cách tính diện tích xung quanh, diện tích toàn phần và thể tích của các hình.
2. Bài tập minh họa
Bài 1: Tính thể tích khối gỗ như hình vẽ:
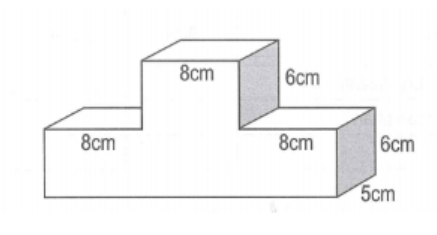
Hướng dẫn: Để tính thể tích của khối gỗ, chúng ta chia hình thành 2 hình hộp chữ nhật nhỏ. Tính thể tích của 2 hình hộp chữ nhật. Thể tích của khối gỗ bằng tổng thể tích của 2 hình nhỏ.
Thể tích của hình hộp chữ nhật nhỏ là:
8 x 5 x 6 = 240 (cm3 )
Thể tích của hình hộp chữ nhật lớn là:
(8 + 8 + 8) x 5 x 6 = 720 (cm3 )
Thể tích của khối gỗ là: 240 + 720 = 960 (cm3 )
Đáp số: 960cm3
Bài 2: Một thùng đựng hàng có nắp dạng hình hộp chữ nhật có chiều dài 2,5m, chiều rộng 1,8m và chiều cao 2m. Người thợ cần bao nhiêu ki-lô-gam sơn để đủ sơn mặt ngoài của thùng? Biết rằng mỗi ki-lô-gam sơn sơn được 5m2mặt thùng.
Hướng dẫn: Đầu tiên ta cần tính diện tích xung quanh, diện tích toàn phần của thùng đựng hàng. Sau đó tính khối lượng số sơn cần dùng.
Diện tích xung quanh thùng đựng hàng là:
(2,5 + 1,8) x 2 x 2 = 17,2 (m2 )
Diện tích 2 đáy của thùng đựng hàng là:
2,5 x 1,8 x 2 = 9 (m2 )
Diện tích toàn phần của thùng đựng hàng là:
17,2 + 9 = 26,2 (m2 )
Khối lượng ki-lô-gam sơn cần dùng là:
26,2 : 5 = 5,24 (kg)
Đáp số: 5,24kg
III/ Bài tập vận dụng
1. Bài tập có lời giải
Bài 1:Cho tam giác ABC. Trên cạnh BC ta lấy 6 điểm. Nối đỉnh A với mỗi điểm vừa chọn. Hỏi đếm được bao nhiêu hình tam giác.
Lời giải:

Ta nhận xét :
- Khi lấy 1 điểm thì tạo thành 2 tam giác đơn ABD và ADC. Số tam giác đếm được là 3 : ABC, ADB và ADC. Ta có : 1 + 2 = 3 (tam giác)
- Khi lấy 2 điểm thì tạo thành 3 tam giác đơn và số tam giác đếm được là 6 : ABC, ABD, ADE, ABE, ADC và AEC. Ta có : 1+ 2 + 3 = 6 (tam giác)
Vậy khi lấy 6 điểm ta sẽ có 7 tam giác đơn được tạo thành và số tam giác đếm được là : 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 (tam giác)
Cách 2:
- Nối A với mỗi điểm D, E, …, C ta được một tam giác có cạnh AD. Có 6 điểm như vậy nên có 6 tam giác chung cạnh AD (không kể tam giác ADB vì đã tính rồi)
- Lập luận tương tự như trên theo thứ tự ta có 5, 4, 3, 2, 1 tam giác chung cạnh AE, AP, …, AI.
- Vậy số tam giác tạo thành là :7 + 6 + 5 + 4 +3 +2 + 1 = 28 (tam giác).
Bài 2:Cho hình chữ nhật ABCD. Chia mỗi cạnh AD và BC thành 4 phần bằng nhau, AB và CD thành 3 phần bằng nhau, rồi nối các điểm chia như hình vẽ.
Ta đếm được bao nhiêu hình chữ nhật trên hình vẽ?

Lời giải:
- Trước hết Ta xét các hình chữ nhật tạo bởi hai đoạn AD, EP và các đoạn nối các điểm trên hai cạnh AD và BC. Bằng cách tương tự như tronh ví dụ 1 ta tính được 10 hình.
- Tương tự ta tính được số hình chữ nhật tạo thành do hai đoạn EP và MN, do MN và BC đều bằng 10.
- Tiếp theo ta tính số hình chữ nhật tạo thành do hai đoạn AD và MN, EP và BC với các đoạn nối các điểm trên hai cạnh AD và BC đều bằng 10.
Vì vậy :
Số hình chữ nhật đếm được trên hình vẽ là :10 + 10 + 10 + 10 + 10 + 10 = 60 (hình)
Đáp số 60 hình.
Bài 3:Cần ít nhất bao nhiêu điểm để khi nối lại ta được 5 hình tứ giác ?

Lời giải:
- Nếu ta chỉ có 4 điểm ( trong đó không có3 điểm nào cùng nằm trên 1 đoạn thẳng) thì nối lại chỉ được 1 hình tứ giác.
- Nếu ta chọn 5 điểm, chẳng hạn A, B, C, D, E (trong đó không có 3 điểm nào nằm trên cùng một đoạn thẳng) thì :
+ Nếu ta chọn A là 1 đỉnh thì khi chọn thêm 3 trong số 4 điểm còn lại B, C, D, E và nối lại ta sẽ được một tứ giác có một đỉnh là A. Có 4 cách chọn 3 điểmtrong số 4 điểm B, C, D, E để ghép với A. Vậy có 4 tứ giác đỉnh A.
- Có 1 tứ giác không nhận A làm đỉnh, dó là BCDE. Từ kết quả trên đây ta suy ra
Khi có 5 điểm ta được 5 tứ giác.
Vậy để có 5 hình tứ giác ta cần ít nhất 5 điểm khác nhau (trong đó không có 3 điểm nào nằm trên cùng một đoạn thẳng)
Bài 4:Cho tam giác ABC có diện tích là 150 cm2. Nếu kéo dài đáy BC (về phía B) 5 cm thì diện tích sẽ tăng thêm 37,5 cm2 . Tính đáy BC của tam giác.

Lời giải:
Cách 1 :Từ A kẻ đường cao AH của ∆ ABC thì AH cũng là đường cao của ∆ ABD
Đường cao AH là : 37,5 x 2 : 5 = 15 (cm)
Đáy BC là : 150 x 2 : 15 = 20 (cm)
Đáp số 20 cm.
Cách 2 :
Từ A hạ đường cao AH vuông góc với BC . Đường cao AH là đường cao chung của hai tam giác ABC và ABD . Mà : Tỉ số 2 diện tích tam giác là :

Hai tam giác có tỉ số diện tích là 4 mà chúng có chung đường cao,nên tỉ số 2 đáy cũng là 4. Với đáy BC là : 5 x 4 = 20 (cm)
Đáp số 20 cm.
Bài 5:Cho tam giác ABC vuông ở A có cạnh AB dài 24 cm, cạnh AC dài 32 cm. Điểm M nằm trên cạnh AC. Từ M kẻ đường song song với cạnh AB cắt BC tại N. Đoạn MN dài 16 cm. Tính đoạn MA.

Lời giải:
Diện tích tam giác NCA là: 32 x 16 : 2 = 256 (cm2)
Diện tích tam giác ABC là :
24 x 32 : 2 = 348 (cm2)
384 – 256 = 128 (cm2)
Chiều cao NK hạ từ N xuống AB là : 128 x 2 : 24= 10 ⅔ (cm)
Vì MN ||AB nên tứ giác MNBA là hình thang vuông. Do vậy MA cũng bằng 10 ⅔cm
Đáp số: 10 ⅔ cm
Bài 6: Cho tam giác ABC vuông ở A. Cạnh AB dài 28 cm, cạnh AC dài 36 cm M là một điểm trên AC và cách A là 9 cm. Từ M kẻ đường song song với AB và đường này cắt cạnh BC tại N. Tính đoạn MN.

Lời giải:
Vì MN||AB nên MN⊥ AC tại M. Tứ giác MNAB là hình
thang vuông. Nối NA. Từ N hạ NH⊥ AB thì NH là chiều cao của tam giác NBA và của hình thang MNBA nên NH = MA và là 9 cm.
Diện tích tam giác NBA là : 28 x 9 : 2 = 126 (cm2)
Diện tích tam giác ABC là : 36 x 28 : 2 = 504 (cm2)
Diện tích tam giác NAC là : 504 – 126 = 378 (cm2)
Đoạn MN dài là : 378 x 2 : 36 = 21 (cm)
2. Bài tập vận dụng
Bài 1: Một tấm bìa hình bình hành có chu vi 4dm. Chiều dài hơn chiều rộng 10cm và bằng chiều cao. Tính diện tích tấm bìa đó.
Bài 2: Một hình vuông có diện tích bằng 4/9 diện tích của một hình bình hành có đáy 25cm và chiều cao 9cm. Tính cạnh của hình vuông.
Bài 3: Một bể bơi có chiều dài 12m, chiều rộng 5m và sâu 2,75m. Hỏi người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh thành bể đó? Biết rằng mỗi viên gạch có chiều dài 25cm, chiều rộng 20 cm và diện tích mạch vữa lát không đáng kể.
Bài 4: Một viên gạch dạng hình hộp chữ nhật có chiều dài 22cm, chiều rộng 10cm, chiều cao 5,5 cm.Tính diện tích xung quanh và diện tích toàn phần của diện tích toàn phần của khối gạch dạng hình hộp chữ nhật do 6 viên gạch xếp thành.
Bài 5: Diện tích hình H đã cho là tổng diện tích hình chữ nhật và hai nửa hình tròn. Tìm diện tích hình H
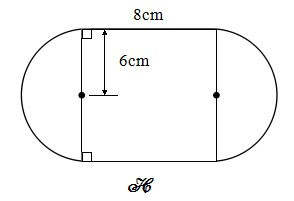
Bài 6: Tính diện tích phần tô đậm hình tròn (xem hình vẽ bên) biết 2 hình tròn có cùng tâm O và có bán kính lần lượt là 0,8 m và 0,5m.
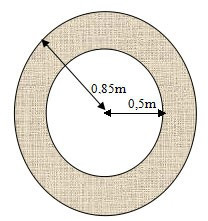
Bài 7: Sân trường em hình chữ nhật có chiều dài 45m và hơn chiều rộng 6,5m. Chính giữa sân có 1 bồn hoa hình tròn đường kính 3,2m. Tính diện tích sân trường còn lại?
Bài 8: Tính diện tích hình thang có đáy lớn bằng 25 m, chiều cao bằng 80% đáy lớn, đáy bé bằng 90% chiều cao.
Bài 9: Có một miếng đất hình bình hành cạnh đáy dài là 32,5m; chiều cao bằng23 cạnh đáy. Trên miếng đất người ta trồng nhau, mỗi mét vuông đất thu hoạch được 2,4kg rau. Hỏi trên miếng đất đó thu hoạch được tất cả là bao nhiêu ki-lô-gam rau ?
Bài 10: Một miếng đất hình thoi có diện tích bằng 288 m2, đường chéo thứ nhất có độ dài 36m, người ta vẽ miếng đất lên bản đồ có tỉ lệ 1 : 400. Hỏi diện tích của hình vẽ trên bản đồ bằng bao nhiêu ?
Bài 11:Cho 5 điểm A, B, C, D, E trong đó không có 3 điểm nào nằm trên cùng một đoạn thẳng. Hỏi khi nối các điểm trên ta được bao nhiêu đoạn thẳng?
Sự đa dạng của các dạng toán trong chương trình học lớp 5 có thể khiến bé choáng ngợp và bối rối. Việc nhận dạng các công thức toán, đặc biệt là các bài toán lớp 5 hình học đôi khi gây trở ngại cho trẻ. Vậy làm cách nào để trẻ cảm thấy tự tin trong quá trình giải toán hình và phân biệt rõ giữa các loại khác nhau? eivonline.edu.vn cùng bé và các bậc phụ huynh đi tìm lời giải đáp ngay bây giờ nhé!
Các dạng toán hình học từ cơ bản đến nâng cao ở lớp 5
Ngoài các dạng bài ôn tập tổng quát và chi tiết nâng cao về các dạng hình phổ biến, học sinh sẽ tập làm quen với các khối hình 3D nâng cao, đồng thời tìm hiểu và đào sâu vào cách tính thể tích của một hình.
Nhận dạng các loại hình học
Trước khi bước đến giai đoạn tính chu vi, diện tích của một hình trong chương trình toán lớp 5 hình học, học sinh cần nắm rõ lý thuyết cách thức nhận dạng một hình cụ thể. Từ đó mới có thể xác định cách tính phù hợp cho từng hình.
Lý thuyết cần nhớHình tam giác là hình có 3 đỉnh và 3 góc.
Hình tứ giác là hình có 4 đỉnh và 4 góc.
Hình vuông được đĩnh nghĩa là hình có 4 góc vuông với 4 cạnh bằng nhau và song song với nhau.
Hình chữ nhật là hình có 4 góc vuông với 2 cặp cạnh bằng nhau.
Các bài tập vận dụngBài 1: Cho tam giác ABC. Trên cạnh BC ta lấy 6 điểm. Sau đó, nối đỉnh A với từng điểm đã vẽ. Hỏi đếm được bao nhiêu hình tam giác.
Bài 2: Cho hình chữ nhật ABCD. Lấy trung điễm trên mỗi cạnh AD và BC sao cho tạo thành 4 cạnh nhỏ bằng nhau. AB và CD cắt chia thành 3 phần bằng nhau. Cuối cùng nối các điểm đã vẽ vào với nhau. Có bao nhiêu hình chữ nhật được tạo thành?
Bài 3: Cho 5 điểm F, G, H, I, J trong đó không có 3 điểm nào nằm trên cùng một đoạn thẳng. Vậy tổng cộng có bao nhiêu đoạn thẳng được tạo thành?
Tính chu vi, diện tích của các hình
Sau đây sẽ là cách tính chu vi và diện tích cho mỗi dạng hình khác nhau mà học sinh sẽ được học trong chương trình toán lớp 5 hình học.
Hình tam giácSau đây là các phép tính công thức và bài tập vận dụng cho cách tính toán diện tích và chu vi hình tam giác.
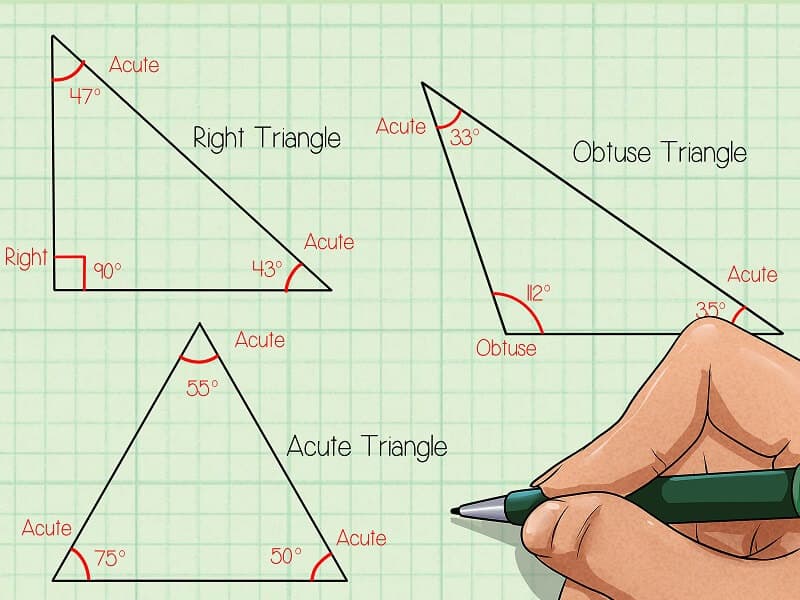
Kiến thức cần nhớTam giác là hình bao gồm 3 cạnh với 3 đỉnh tạo thành một tam giác. Đỉnh là điểm mà hai cạnh gặp nhau. Cả 3 cạnh đều có thể dùng làm đế.
Đường cao của tam giác là đoạn thẳng hạ từ trên xuống và vuông góc với đáy. Do đó, mỗi tam giác có 3 đường cao.
Công thức tính chu vi và diện tích của một hình tam giác đã cho 3 cạnhChu vi tam giác: C = a + b + c
Trong đó a, b, c lần lượt là chiều dài 3 cạnh của tam giác.
Diện tích tam giác: S = (a x h) / 2
Trong đó:
a: Chiều dài đáy tam giác (đáy là một trong 3 cạnh của tam giác tùy theo quy đặt của người tính)h: Chiều cao của tam giác, ứng với phần đáy chiếu lên (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy, đồng thời vuông góc với đáy của một tam giác)Bài tập vận dụngBài 1: Tính diện tích hình tam giác khi cho biết :
a, Độ dài đáy là 17cm và chiều cao là 13cm
b, Độ dài đáy là 8m và chiều cao là 5,5m
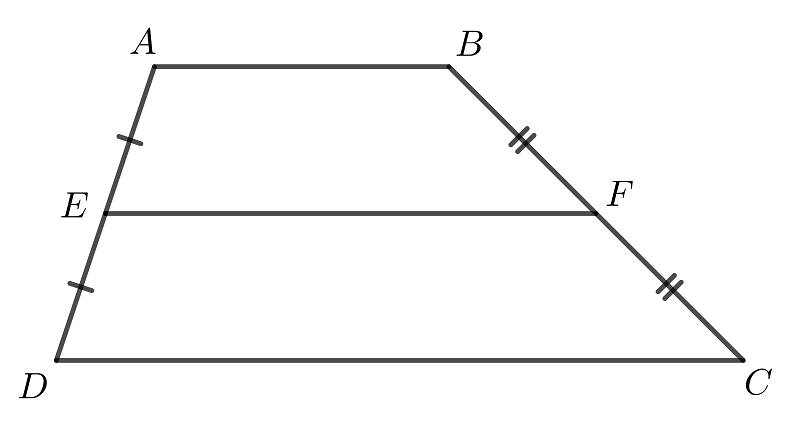
Vậy còn hình thang, làm cách nào để tính được chu vi và diện tích hình thang theo như hướng dẫn của toán lớp 5 hình học?
Kiến thức cần nhớHình thang là tứ giác lồi với đặc điểm nhận dạng là hai cạnh đối song song. Hai cạnh này được quy ước là hai cạnh đáy của một hình thang. Hai cạnh còn là được gọi là cạnh bên.
Công thức tính chu vi và diện tích hình thangDiện tích hình thang: S = h × ((a + b)/2)
Trong đó:
a và b: Chiều dài đáy của hình thangh: Chiều cao của hình thang, ứng với phần đáy chiếu lên (chiều cao hình thang bằng đoạn thẳng hạ từ đỉnh xuống đáy, đồng thời vuông góc với đáy của hình thang đó)Chu vi hình thang: P = a + b + c + dTrong đó: a, b, c và d là cạnh của hình thang
Bài tập vận dụngBài 1: Cho hình thang ABCD có độ dài đường cao là 4,2 dm, diện tích = 36,12 dm2 và đáy lớn CD dài hơn đáy bé AB là 7,8 dm. Kéo dài AD và BC cắt nhau tại E. Biết AD = 3/5 DE. Tính diện tích tam giác ABE với các dữ liệu đã cho trên.
Bài 2: Cho hình thang ABCD. Bốn điểm M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Biết diện tích tứ giác MNPQ là 115 cm2. Tính diện tích hình thang ABCD.
Phụ huynh có thể đặt ra câu đố về cách tính chu vi và diện tích hình tròn cho các bé. Đây sẽ là câu hỏi thú vị giúp bé ôn lại kiến thức đồng thời thoải mái chia sẻ và chủ động trong việc học hơn.
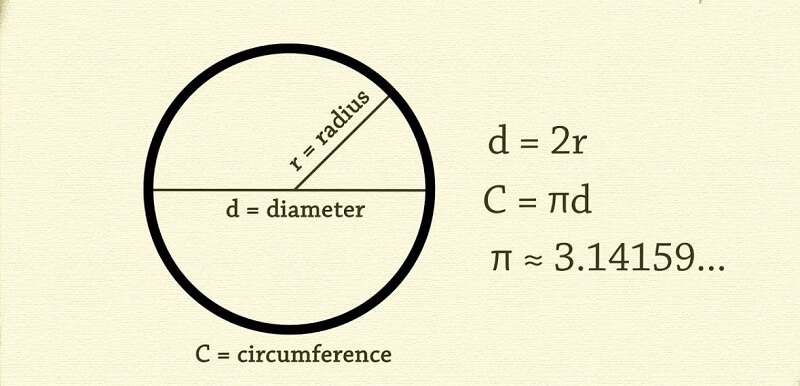
Kiến thức cần nhớTrên mặt phẳng, hình tròn là diện tích trên mặt phẳng nằm "trong" một hình tròn. Chu vi, bán kính và tâm của một hình tròn là tâm và bán kính của hình tròn bao quanh nó.
Công thức tính chu vi và diện tích của một hình tròn cho biết đường kính và bán kínhChu vi hình tròn: C= d x Pi hoặc C = (r x 2) x Pi.
Trong đó:
C: chu vi hình tròn.
d: đường kính hình tròn.
Pi: Số Pi (~3,141...).
r: bán kính hình tròn.
Diện tích hình tròn: S = Pi x r2Trong đó:
S: diện tích hình tròn.
Pi: Số Pi (~3,141...).
r: bán kính hình tròn.
Bài tập vận dụngBài 1: Có một hình tròn C có đường kính bằng 10cm. Hỏi chu vi hình tròn C bằng bao nhiêu?
Bài 2: Tính diện tích hình tròn khi biết chu vi hình tròn đó là 15,7cm.
Hình học phẳng
Có điều gì mà học sinh cần lưu ý khi thực hiện các bài tập toán hình học phẳng hay không? Cùng eivonline.edu.vn tìm hiểu ngay sau đây nhé!
Lý thuyết cần nhớBài toán hình học phẳng được chia thành hai dạng nhỏ:
Các bài toán không có nội dung thực tế: các bài toán về mảnh đất, số liệu và cách tính diện tích, chu vi hoặc một cạnh nào đó ...
Câu hỏi có nội dung thực tế: Trong các câu hỏi đều có dữ liệu liên quan đến thực tế cuộc sống.
Đối với môn toán này, chúng ta cần ghi nhớ và vận dụng các công thức tính chu vi, diện tích các hình phẳng đã học: hình vuông, hình chữ nhật, hình tam giác, hình tròn, hình thang, hình bình hành.
Các bài tập vận dụngBài 1: Một thửa ruộng có dạng hình thang với chiều dài đáy lớn là 120m. Biết đáy bé có chiều dài ngang bằng đáy lớn. Đáy bé dài hơn chiều cao 5m. Cứ 100m2 trung bình thì người nông dân thu về được 72kg thóc. Hỏi người nông dân thu về được bao nhiêu kg thóc trên thửa ruộng hình thang trên.
Bài 2: Ta có một tấm bìa hình bình hành được tính với chu vi 4dm. Với các số đo bao gồm chiều dài hơn chiều rộng 10cm. Ngoài ra chiều dài cũng ngang bằng chiều cao. Tính diện tích tấm bìa đó.
Bài 3: Một hình vuông có diện tích bằng 4/9 diện tích của một hình bình hành có đáy 25cm và chiều cao 9cm. Tính cạnh của hình vuông.
Diện tích và thể tích hình khối
Khác so với các hình bề mặt phẳng, cách tính hình khối có một sự khác biệt nhất định. Trong quá trình học toán lớp 5 hình học, đặc biệt là hình khối, học sinh cần lưu ý kỹ những điều sau.
Hình lập phươngHình lập phương là gì và cách tính hình lập phương như thế nào? Các bậc phụ huynh cùng con trẻ khám phá ngay nhé!
Lý thuyết cần nhớHình lập phương là hình lập phương có 6 mặt, 8 đỉnh, 12 cạnh và tất cả các mặt đều là hình vuông có các cạnh bằng nhau. Hoặc hình lập phương còn là một khối hình có chiều dài, chiều rộng và chiều cao bằng nhau.
Công thức tính toán diện tích và thể tích một hình lập phươngThể tích của một hình lập phương: V = a x a x a = a3
Trong đó: a: các cạnh của một hình lập phương.
Diện tích xung quanh của một hình lập phương: Sxq = 4 x a²Trong đó:
Sxq: Diện tích xung quanh.
a: các cạnh của hình lập phương
Diện tích toàn phần của một hình lập phương: Stp = 6 x a²Trong đó:
Stp: Diện tích toàn phần.
a: các cạnh của hình lập phương.
Các bài tập vận dụngBài 1: Có một hình lập phương 6 cạnh ABCDEF với các cạnh đều có kích thước bằng nhau với chiều dài là 5cm . Hỏi diện tích và thể tích của hình lập phương này bằng bao nhiêu?
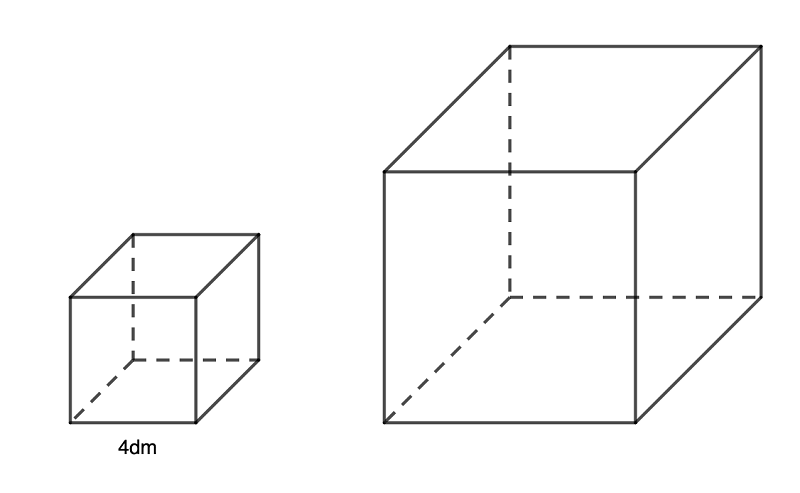
Ngoài hình lập phương, bé cũng sẽ bắt đầu tìm hiểu về dạng hình trụ trong chương trình toán lớp 5 hình học. Vậy các công thức liên quan đến hình trụ bao gồm những gì?
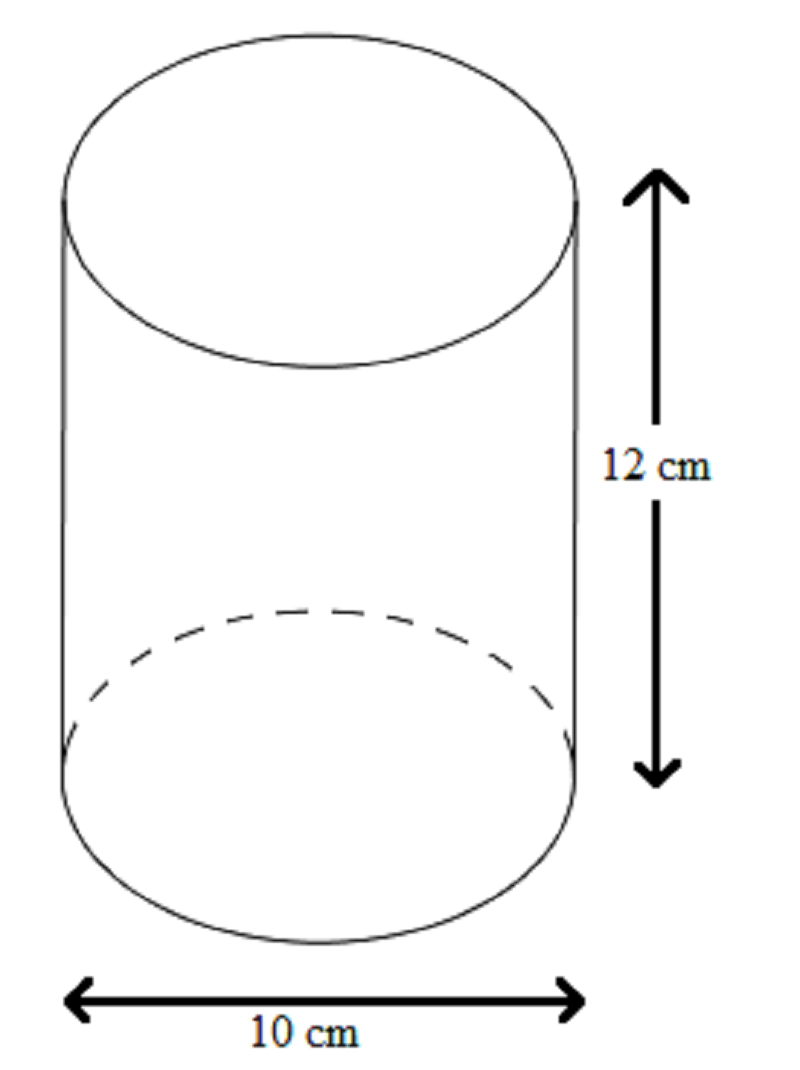
Lý thuyết cần nhớHình trụ là hình được bao bởi một hình trụ và hai đường tròn có đường kính bằng nhau.
Công thức tính diện tích và thể tích hình trụCông thức tính thể tích hình trụ: V=π∗r2∗h=3.14∗r2∗h=Sđáy∗h
Trong đó:
R: bán kính hình trụ.
H: chiều cao
Π: hằng số (π = 3,14).
Sđáy: diện tích mặt đáy của hình trụ.
Công thức tính diện tích xung quanh của một hình trụ: Sxq = 2.π.r.hTrong đó:
r: Bán kính hình trụ.
h: Chiều cao nối từ đáy tới đỉnh hình trụ.
π = 3.14
Bài tập vận dụngBài 1: Tính diện tích xung quanh, diện tích toàn phần và cả thể tích của một hình trụ, biết:
a) Bán kính đáy 4cm, chiều cao 5cm.
Xem thêm: Cách sửa định dạng ngày tháng trong excel cực đơn giản, sửa lỗi sai định dạng ngày, tháng trên excel
b) Bán kính đáy 5dm, chiều cao 1,4dm
c) Bán kính đáy 1/2m, chiều cao 1/4m
Hy vọng rằng với nguồn kiến thức eivonline.edu.vn cung cấp, bé đã có thể luyện tập và trau dồi kỹ năng giải toán lớp 5 hình học khoa học và hiệu quả hơn. eivonline.edu.vn cùng bé đồng hành trong mọi chặng đường giải toán.