Sách Luyện Thi THCS, Chuyên
Sách mầm non - tè Học
Sách Anh Văn
Sách tiếng Trung
Sách giờ Nhật
HASH TAG
#3 step#big step#mega 2021#aha#workbook#Sách Toán#Sách tiếng Anh#Vật Lý#Hóa Học#Luyện thi thpt Quốc Gia#Mega luyện đề#Trắc nghiệm toán#Sinh học tậpBài 1: một cái hộp đựng 6 viên bi đỏ và 4 viên bi xanh.Lấy theo lần lượt 2 viên bi từ mẫu hộpđó.Tính xác xuất nhằm viên bi được mang lần thứ hai là bi xanh.Hướng dẫn* Số biện pháp lấy lần lượt 2 viên bi từ vỏ hộp là 10.9 = 90 (cách)* ví như lần 1 đem được bi đỏ cùng lần 2 lấy được bi xanh thì bao gồm 6.4 = 24 (cách)* giả dụ lần 1 đem được bi xanh và lần 2 cũng chính là bi xanh thì có 4.3 = 12 (cách)Suy ra tỷ lệ cần tìm là
( 24 + 12) 4p = =90 10
Bài 2: Một hộp đựng 10 viên bi đỏ, 8 viên bi vàng cùng 6 viên bi xanh. Lấy bỗng dưng 4viên bi. Tính tỷ lệ để những viên bi rước được đủ cả 3 màu.Hướng dẫn
Tổng số viên bi trong hộp là 24. Call Ω là không gian mẫu.Lấy hốt nhiên 4 viên trong vỏ hộp ta có C 4cách đem hay n( Ω ) = C 4 .Gọi A là vươn lên là cố đem được các viên bi tất cả đủ cả 3 màu. Ta có những trường hợp sau:+) 2 bi đỏ, 1 bi vàng cùng 1 bi xanh: bao gồm C 2 C1C1 = 2160 cách+) 1 bi đỏ, 2 bi vàng và 1 bi xanh: gồm C1 C 2C1 = 1680 cách+) 1 bi đỏ, 1 bi vàng và 2 bi xanh: tất cả C1 C1C 2 = 1200cách
Do đó, n(A) = 5040Vậy, xác suất biến cố A là
P( A) = n( A) = 5040n(Ω) 10626≈ 47, 4%
Bài 3: Từ những chữ số của tập
T = 0;1; 2; 3; 4; 5 , tín đồ ta ghi đột nhiên hai số trường đoản cú nhiêncó tía chữ số không giống nhau lên hai tấm thẻ. Tính tỷ lệ để nhì số ghi trên hai tấm thẻ đó cóít nhất một số chia hết đến 5.Hướng dẫn+ gồm 5.A2 = 100số thoải mái và tự nhiên có 3 chữ số khác nhau+ Có
A2 + 4.A1 =36
số tự nhiên và thoải mái có 3 chữ số không giống nhau và phân chia hết đến 5.
Bạn đang xem: Toán xác suất có lời giải
+ có 64 số tự nhiên có 3 chữ số khác biệt và không chia hết đến 5.+ n (Ω) =C1
.C1= 9900100 99
+ call A là trở thành cố : “Trong nhì số được ghi bên trên 2 tấm thẻ có ít nhất một số chia hết đến 5”
Ta có:n ( A) =C1
.C1+C1.C1= 3564
Vậy :36 64 36 35P ( A) = n ( A) = 3564 = 9 = 0, 36
n (Ω)
20
10 5 5
9900 25Bài 4: Có trăng tròn tấm thẻ được tấn công số từ một đến 20. Chọn tự dưng ra 5 tấm thẻ. Tính xácsuất để trong 5 tấm thẻ được lựa chọn ra có 3 tấm thẻ sở hữu số lẻ, 2 tấm thẻ với số chẵntrong kia chỉ tất cả đúng một lớp thẻ với số phân chia hết cho 4.Hướng dẫn- Số bộ phận của không khí mẫu là:n (Ω) = C5
= 15504 .
- Trong đôi mươi tấm thẻ, có 10 tấm thẻ với số lẻ, bao gồm 5 tấm thẻ mang số chẵn và chia hết cho4, 5 tấm thẻ có số chẵn với không chia hết mang đến 4.- điện thoại tư vấn A là trở nên cố buộc phải tính xác suất. Ta có:n ( A) = C 3 .C1.C1 = 3000 .Vậy, phần trăm cần tính là:P ( A) = n ( A) = 3000 = 125 .
n (Ω)= 995
A 415504 646Bài 5: điện thoại tư vấn M là tập hợp những số tự nhiên gồm 9 chữ số không giống nhau. Chọn bỗng nhiên mộtsố trường đoản cú M, tính xác suất để số được chọn bao gồm đúng 4 chữ số lẻ cùng chữ số 0 đứng thân hai chữsố lẻ (các chữ số tức tốc trước và liền sau của chữ số 0 là các chữ số lẻ).Hướng dẫn
Xét những số gồm 9 chữ số không giống nhau:- bao gồm 9 phương pháp chọn chữ số tại phần đầu tiên.- Có
A8 phương pháp chọn 8 chữ số tiếp theo
Do đó số những số bao gồm 9 chữ số khác nhau là: 9. A8 = 3265920Xét những số vừa lòng đề bài:- gồm C 4 cách chọn 4 chữ số lẻ.- Đầu tiên ta xếp vị trí cho chữ số 0, vị chữ số 0 không thể mở màn và cuối nên tất cả 7cách xếp.- tiếp theo ta có2 cách chọn cùng xếp hai chữ số lẻ đứng 2 bên chữ số 0.- sau cùng ta bao gồm 6! cách xếp 6 chữ số sót lại vào 6 vị trí còn lại.Gọi A là trở thành cố đang cho, lúc ấy n( A) = C 4 .7.A2 .6!= 302400.5 4Vậy tỷ lệ cần tìm kiếm là
P( A) = 302400 = 5 .3265920 54
11
5 6 5 6
16
Bài 6: một nhóm có 5 học sinh nam cùng 6 học viên nữ. Cô giáo chọn thốt nhiên 3 học sinhđể làm trực nhật. Tính tỷ lệ để 3 học sinh được chọn tất cả cả nam cùng nữ.Hướng dẫn- Ta cón (Ω) = C3
= 165
- Số biện pháp chọn 3 học viên có cả phái mạnh và thiếu phụ là C 2 .C1 + C1.C 2 = 135- vì đó xác suất để 3 học sinh được chọn tất cả cả phái nam và chị em là 135 = 9165 11
Bài 7: Hai fan cùng bắn vào một trong những mục tiêu. Phần trăm bắn trúng của từng fan là 0,8 và0,9. Tìm tỷ lệ của những biến cố sao cho chỉ bao gồm một bạn bắn trúng mục tiêu.Hướng dẫn- điện thoại tư vấn A là vươn lên là cố của tín đồ bắn trúng kim chỉ nam với phần trăm là 0.8- B là phát triển thành cố của người bắn trúng kim chỉ nam với xác suất là 0.9- gọi C là biến chuyển cố phải tính phần trăm thì C = A.B + A.BVậy phần trăm cần tính là P(C)=0,8.(1-0,9)+(1-0,8).0,9=0,26Bài 8: một đội ngũ cán bộ khoa học gồm 8 nhà toán học nam, 5 nhà đồ vật lý phái nữ và 3 nhàhóa học tập nữ. Chọn ra từ kia 4 người, tính phần trăm trong 4 người được chọn buộc phải có nữ vàcó đủ ba bộ môn
Hướng dẫn
Ta có : Ω = C 4= 1820Gọi A: “2nam toán, 1 lý nữ, 1 hóa nữ”B: “1 phái nam toán, 2 lý nữ, 1 hóa nữ”C: “1 nam toán, 1 lý nữ, 2 hóa bạn nữ “Thì H = A ∪ B ∪ C : “Có bạn nữ và đủ ba bộ môn”C 2C1C1 + C1C 2C1 + C1C1C 2 3P(H ) = 8 5 3 8 5 3 8 5 3 =Ω 7
Bài 9: một đội có 5 học sinh nam với 6 học viên nữ. Cô giáo chọn bỗng nhiên 3 học tập sinhđể làm cho trực nhật. Tính tỷ lệ để 3 học sinh được chọn bao gồm cả nam và nữ.
Xác suất có đk là kỹ năng xảy ra của một trở nên cố dựa trên một phát triển thành cố như thế nào đó. Sau đây eivonline.edu.vn xin phép được gửi đến bạn một số bài tập tỷ lệ có điều kiện trong môn Xác suất thống kê giúp cho bạn nắm vững kiến thức và kỹ năng phần này nhé.
1. Tỷ lệ có điều kiện là gì?
Xác suất tất cả điều kiện(Conditional probability) là phần trăm của một đổi mới cố A như thế nào đó khi biết rằng một đổi thay cố B không giống xảy ra. Ký hiệu P(A|B) , và đọc là “xác suất của A, biết B“.1.1 Công thức phần trăm có điều kiện

Trong đó biến chuyển cố A đã xẩy ra trước, còn đổi mới cố B xẩy ra sau và P(A) >0.
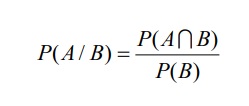
Trong đó trở thành cố B đã xẩy ra trước, còn đổi thay cố A xẩy ra sau cùng P(B) >0. Trường hợp quan trọng đặc biệt khi không gian mẫu có các kết quả đồng kĩ năng thì:
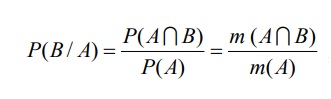
Trong kia m (A∩B)là số những trường hợp dễ dãi của (A∩B); m(A) là số các trường hợp dễ dàng của A.
1.2 Ví dụ tỷ lệ có điều kiện
Ví dụ : Gieo thứu tự hai nhỏ xúc xắc phẳng phiu và đồng chất. Tính phần trăm để tổng cộng chấm xuất hiện trên hai nhỏ xúc xắc bằng 6. Biết rằng bé xúc xắc thứ nhất xuất hiện tại mặt 4 chấm.
Ký hiệu A là biến cố “con xúc xắc trước tiên xuất hiện tại mặt 4 chấm” và B là trở thành cố “ tổng cộng chấm xuất hiện thêm trên 2 bé xúc xắc bởi 6”. Như vậy A xẩy ra trước B.
Khi nhỏ xúc xắc lộ diện mặt 4 chấm (biến nỗ lực A sẽ xảy ra) thì phần trăm để tổng số chấm lộ diện trên hai con xúc xắc bởi 6 được hotline là tỷ lệ điều kiện của đổi thay cố B khi phát triển thành cố A vẫn xảy ra. Ký hiệu là P(B/A). Khi bé xúc xắc trước tiên đã xuất hiện thêm mặt 4 chấm thì không gian mẫu sẽ chỉ với 6 tác dụng (6 đổi thay cố) sau đây: (4,1); (4,2); (4,3); (4,4); (4,5); (4,6). Suy ra P(B/A) = P(4,2)=1/6 .
1.3 phương pháp nhân phần trăm có điều kiện
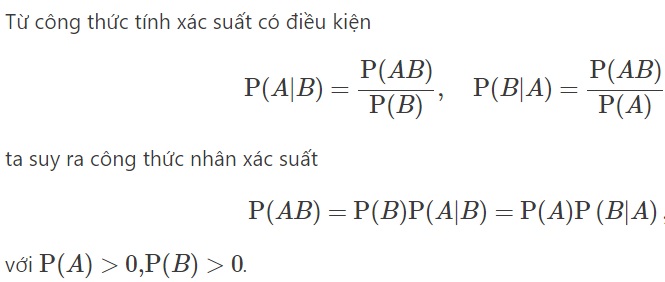
2. Phân biệt tỷ lệ thông hay và tỷ lệ có điều kiện
Một giữa những các dễ ợt nhất để nhận thấy xác suất thường thì hay xác suất có điều kiện là:
Câu hỏi cất từ khoá: biết rằng, nếu, khi,… VD: Biết công ty thắng thầu dự án công trình 1, tìm tỷ lệ công ty win thầu dự án công trình 2Đề bài xích cho lần lượt khả năng A, B. VD: kĩ năng thắng thầu của những dự án theo thứ tự là 0,4 cùng 0,5.3. Những dạng bài tập tỷ lệ có điều kiện
3.1 Tính xác suất có điều kiện các biến vắt độc lập
Bài 1: Một doanh nghiệp đấu thầu 2 dự án độc lập. Khả năng thắng thầu của những dự án theo lần lượt là 0,4 với 0,5.a)Tìm xác suất công ty thắng thầu đúng 1 dự ánb) Biết doanh nghiệp thắng thầu dự án công trình 1, tìm tỷ lệ công ty chiến thắng thầu dự án 2c) Biết doanh nghiệp không win thầu dự án công trình 1, tìm xác suất công ty thắng thầu dự án 2
Giải
Gọi A là vươn lên là cố”thắng thầu dự án 1″
B là vươn lên là cố”thắng thầu dự án 2″ nhưng theo đề bài bác P(A)= 0,4 , P(B)=0,5, 2 đổi thay cố A,B độc lập
a) hotline A1 là biến đổi cố “thắng thầu đúng 1 dự án”(P(A1)=P(A overlineB+ overlineAB))(= P(A overlineB) +P(overlineAB))(P(A1)=P(A).P( overlineB)+ P(overlineA)P(B))(= 0,4.(1-0,5)+ (1-0,4).0,5=0,5)
b) điện thoại tư vấn B1 là biến chuyển cố “thắng thầu dự án công trình thứ 2 biết thắng thầu dự án công trình 1”
P(B1)=P(B|A)= P(B)=0,5 (do A,B độc lập)
c) điện thoại tư vấn C1 là đổi mới cố “thắng thầu dự án 2 biết không chiến thắng thầu dự án 1”
(P(C1)=P(B|overlineA)=P(B)=0,5)3.2 Tính tỷ lệ điều kiện các biến nắm bất kỳ
Bài 2: Một công ty đấu thầu 2 dự án. Kĩ năng thắng thầu của những dự án theo thứ tự là 0,4 cùng 0,5. Kĩ năng thắng thầu của 2 dự án công trình là 0,3. điện thoại tư vấn A, B thứu tự là vươn lên là cố chiến hạ thầu dự án công trình 1 và dự án công trình 2.a) A cùng B có chủ quyền không?b) Tìm xác suất công ty chiến hạ thầu đúng dự án công trình 1c) Biết doanh nghiệp thắng thầu dự án 1, tìm tỷ lệ công ty thắng thầu dự án 2d) Biết doanh nghiệp không thắng thầu dự án công trình 1, tìm xác suất công ty chiến hạ thầu dự án 2
Giải
Tóm tắt đề bài: P(A)=0,4 , P(B)=0,5 , P(AB)=0,3
a) A,B tự do => P(AB)= P(A).P(B)
mà 0,3 ≠0,4×0,5 => A, B không độc lập(phụ thuộc)
b) điện thoại tư vấn B1 là thay đổi cố chiến thắng thầu đúng 1 dự án
(P(B1)=P(AoverlineB)+P(overlineAB))(=P(A)-P(AB)+P(B)-P(AB))(=P(A)+P(B)-2P(AB)=0,3)
c) điện thoại tư vấn C1 là thay đổi cố chiến hạ dự 2 biết thắng dự án công trình 1
(P(C1)=P(B|A)=fracP(AB)P(A)=frac0,30,4=0,75)d) call D1 là đổi thay cố “thắng dự án 2 biết ko thắng dự án 1”
(P(D1)=P(B|overlineA)=fracP(overlineAB)P(overlineA)=fracP(B)-P(AB)1-P(A))(=frac0,5-0,31-0,4=frac13)
Bài 3: Một sinh viên làm 2 bài tập kế tiếp. Xác suất làm đúng bài trước tiên là 0,7. Nếu làm đúng bài trước tiên thì kỹ năng làm đúng bài thứ hai là 0,8, tuy nhiên nếu có tác dụng sai bài bác thứ 1 thì kĩ năng làm đúng bài thứ hai là 0,2. Tính xác suấta) làm đúng ít nhất 1 bàib) có tác dụng đúng bài bác 1 hiểu được làm đúng bài bác 2c) có tác dụng đúng cả 2, biết rằng làm đúng một bài
GiảiGọi A1 là biến hóa cố làm đúng bài bác 1Gọi A2 là đổi thay cố làm cho đúng bài 2a) có tác dụng đúng ít nhất 1 bài(P(A1+A2)= 1-P(overlineA1+A2))(= 1-P(overlineA1.overlineA2))(=1-P(overlineA1)P(overlineA2|overlineA1)=0,76)b) có tác dụng đúng bài xích 1 hiểu được làm đúng bài bác 2(P(A1.A2)= P(A1).P(A2|A1)=0,7.0,8)(P(A1+A2)= P(A1)+P(A2)-P(A1A2))(0,76= 0,7+P(A2)- 0,7.0,8)(=>P(A2)=0,62)(P(A1|A2)= fracP(A1A2)P(A2))(=fracA1)P(A2)=0,903)c) làm đúng cả 2 biết rằng làm cho đúng ít nhất 1 bài(P(A1A2|(A1+A2))= fracP<(A1A2).(A1+A2)>P(A1+A2))(= fracP<(A1A1A2)+(A1A2A2)>P(A1+A2))(=fracP<(A1A2)+(A1A2)>P(A1+A2))(= fracP(A1A2)P(A1+A2)=0,737)
3.3 bài tập cách làm nhân xác suất có điều kiện
Bài 4: Có trăng tròn phế phẩm trong 100 sản phẩm. Chọn thiên nhiên lần lượt ra 2 sản phẩm. Tính xác suất:a. Sản phẩm đầu tiên là phế phẩm.b. Thành phầm thứ hai là phế truất phẩm lúc sản phẩm trước tiên là phế phẩm.c. Cả nhị sản phẩm mang ra đều là phế phẩm
Giải
Gọi A1 là sản phẩm lôi ra lần thứ một là phế phẩm, A2 là sản phẩm lôi ra lần thứ 2 là phế phẩm
a)(P(A)=P(A1.A2+A1 overlineA2))(=P(A1.A2)+P(A1 overlineA2))(=P(A1).P(A2)+P(A1).P(overlineA2))(=fracC_20^1C_100^1.fracC_19^1C_99^1+fracC_20^1C_100^1.(1-fracC_19^1C_99^1)=0,2)b)(P(B)=P(A2|A1))(=fracP(A1A2)PA1)(=P(A2)=fracC_19^1C_99^1=frac1999)c)(P(C)=P(A1.A2)=P(A1).P(A2))(=fracC_20^1C_100^1.fracC_19^1C_99^1=frac19495)
Bài 5: Có nhì hộp đựng sản phẩm. Hộp thứ nhất có 7 thành phầm loại I cùng 3 thành phầm loại II; hộp sản phẩm công nghệ hai tất cả 8 thành phầm loại I với 4 sản phẩm loại II. Từ bỏ mỗi vỏ hộp chọn tự dưng ra một sản phẩm. Tính xác suất:a. Rước được 2 phẩm các loại Ib. Rước được ít nhất một phẩm nhiều loại I.c. Mang được 2 sản phẩm cùng loại.d. Nếu từ hộp đầu tiên lấy tình cờ ra 2 thành phầm và từ hộp sản phẩm công nghệ hai lấy tự dưng ra 1 mặt hàng thì phần trăm lấy được cả ba thành phầm đều là sản phẩm loại I bằng bao nhiêu? xác suất để 3 sản phầm cùng các loại là bao nhiêu?
Giải
a) gọi A là phát triển thành cố “Lấy được 2 sản phẩm loại I”A1 là vươn lên là cố “lấy được một loại sản phẩm từ loại I từ vỏ hộp I”A2 là biến cố “lấy được một mặt hàng từ loại I từ hộp II”=> A = A1.A2 => (P(A)= P(A1A2)= P(A1).P(A2))(= frac710. frac812= 0.46)b) call B là vươn lên là cố “lấy được ít nhất một sản phẩm loại I”(overlineB) là đổi thay cố “lấy được 2 sản phẩm loại II”(overlineB1) là vươn lên là cố “lấy được một sản phẩm từ nhiều loại II từ vỏ hộp I”(overlineB2) là phát triển thành cố “lấy được 1 sản phẩm từ các loại II từ hộp II”=> (P(B)= 1 – P(overlineB) = 1-P(overlineB1.overlineB2))(= 1 -(frac310. frac412)=0.9)c) gọi C là biến đổi cố”lấy được 2 sản phẩm cùng loại”(P(C)= P(A∪overlineB)= P(A)+P(overlineB))(=0,46+0,9=1,36)d) gọi E là trở thành cố “lấy 3 thành phầm loại I”E1 là biến cố “lấy được 2 thành phầm từ một số loại I từ vỏ hộp I”E2 là đổi thay cố “lấy được 1 sản phẩm từ nhiều loại I từ hộp II”=> E=E1.E2 => (P(E)= P(E1.E2)= P(E1).P(E2))(= fracC_7^2C_10^2. fracC_8^1C_12^1= 0,31)Gọi F là biến đổi cố “lấy 3 thành phầm loại II”F1 là vươn lên là cố “lấy được 2 sản phẩm từ các loại II từ vỏ hộp I”F2 là biến hóa cố “lấy được một mặt hàng từ một số loại II từ hộp II”=> F=F1.F2 => (P(F)= P(F1.F2)= P(F1).P(F2))(= fracC_3^2C_10^2. fracC_4^1C_12^1= .0,02)Gọi D là đổi thay cố “lấy 3 sản phẩm cùng loại”P(D)=P(E∪F)=P(E)+P(F)= 0,31+0,02=0,33
Bài 6: Hoạt đụng của một khối hệ thống thông tin có 3 giai đoạn: Mã hóa, truyền tin với giải mã. Một tin nhắn có phần trăm bị lỗi trong quá trình mã hóa là 0,5%; trong giai đoạn truyền tin là 1% cùng trong giai đoạn giải mã là 0,1%. Mang sử các lỗi xẩy ra ở các giai đoạn là độc lập.a. Xác suất để một tin nhắn không xẩy ra lỗi là bao nhiêu?b. Tỷ lệ để một tin nhắn bị lỗi ở quá trình mã hóa hoặc giai đoạn lời giải là bao nhiêu?
Giải
a)Gọi A là phát triển thành cố”tin nhắn không trở nên lỗi”A1 là trở thành cố “tin nhắn bị lỗi ở quá trình mã hoá”A2 là phát triển thành cố “tin nhắn bị lỗi ở quy trình truyền tin”A3 là đổi mới cố “tin nhắn bị lỗi ở quy trình tiến độ giải mã”(A=overlineA1.overlineA2.overlineA3)(=>P(A)=P(overlineA1).P(overlineA2).P(overlineA3))(=0,95.0,99.0,99=0,984)b)Gọi B là trở nên cố “tin nhắn bị lỗi ở quy trình mã hoá hoặc quá trình giải mã”B= A1∪A3=> P(B)=P(A1∪A3)= P(A1)+P(A3)-P(A1A3)= 0,5%+0,1%-(0,5%.0,1%)=0,00599
Bài 7: Một phòng tất cả 3 sản phẩm tính chuyển động độc lập. Tỷ lệ hỏng trong một mon của từng máy khớp ứng là 0,1; 0,2; 0,3. Tính xác suất:a. Cả cha máy lỗi trong tháng.b. Bao gồm một sản phẩm công nghệ hỏng vào tháng.c. Bao gồm hai thứ hỏng vào tháng.d. Có ít nhất một vật dụng hỏng vào tháng.e. đồ vật thứ tía bị hỏng. Biết rằng trong tháng có 2 thiết bị bị hỏng.
Xem thêm: Top 10 Nhà Nghỉ Hà Tiên Giá Rẻ Đẹp Gần Trung Tâm Gần Biển Tốt Nhất
Giải
a)Gọi A là đổi thay cố “cả 3 máy hỏng vào tháng”P(A)=0,1.0,2.0,3=0,006b)Gọi B là vươn lên là cố “có một thứ hỏng trong tháng”Có đúng 1 sản phẩm công nghệ hỏng=>Xảy ra 3 TH:+) TH1: đồ vật 1 hỏng, sản phẩm 2,3 bình thường=>P1=0,1.(1-0,2).(1-0,3)=0,056+) TH2: sản phẩm 1,3 bình thường, thứ 2 hỏng=>P2=(1-0,1).0,2.(1-0,3)=0,126+) TH3: vật dụng 1,2 bình thường, đồ vật 3 hỏng=>P3=(1-0,1).(1-0,2).0,3=0,216=>P(B)=P1+P2+P3=0,398c) gọi C là trở thành cố “có 2 sản phẩm hỏng trong tháng”Có đúng 2 lắp thêm hỏng=>Xảy ra 3 TH:+) TH1: vật dụng 1 hoạt động bình thường, máy 2,3 hỏng=>P1(C)=(1-0,1).0,2.0,3=0,054+) TH2: vật dụng 1,3 hỏng, đồ vật 2 bình thường=>P2(C)=0,1.(1-0,2).0,3=0,024+) TH3: vật dụng 1,2 hỏng, thứ 3 bình thường=>P3(C)=0,1.0,2.(1-0,3)=0,014=>P(C)=P1(C)+P2(C)+P3(C)=0,092d) call (overlineD) là biến hóa cố”không bao gồm máy như thế nào hỏng”,D là đổi thay cố có ít nhất một thứ bị hỏng(P(D)=1-P(overlineD))(= 1 – <(1-0,1).(1-0,2).(1-0,3)>)(=0,496)e) (P(E)= P(P1(C)∪P2(C)|P(C)))(=fracP1(C)∪P2(C)P(C))(=frac0,054+0,0240,092)(=0,85)
Hy vọng qua nội dung bài viết trên eivonline.edu.vn đang cung cấp cho mình đủ tin tức giúp bạn giải bài bác tập xác suất có điều kiện một cách dễ dàng nhất. Cảm ơn các bạn đã tìm hiểu thêm tài liệu trên eivonline.edu.vn.