Cực trị của hàm số là giá bán trị nhưng hàm số thay đổi chiều phát triển thành thiên lúc qua đó. Trong hình học, nó biểu diễn khoảng cách lớn tuyệt nhất từ đặc điểm này sang điểm kia và khoảng tầm cách nhỏ dại nhất từ đặc điểm này sang điểm nọ. Ở lịch trình toán 12 họ sẽ khám phá sâu xa về lý thuyết cực trị và khai thác nhiều dạng bài xích tập khác nhau. Đây cũng là trong những điểm kiến thức rất là quan trọng trong kỳ thi THPTQG trong năm qua. Nội dung bài viết sau đây, Verba
Learn để giúp đỡ bạn đọc nắm vững điểm kiến thức và kỹ năng này thông qua phần lý thuyết, phân dạng bài xích tập và một vài tài liệu cung cấp học tập.
Bạn đang xem: Bài tập vận dụng liên quan đến hàm số và đồ thị hàm số đồ thị đạo hàm
Mục lục
Tổng quan tiền lý thuyết
Khái niệm cực trị được hiểu đơn giản như sau: cực trị của hàm số là điểm có giá chỉ trị lớn số 1 so với bao quanh và giá bán trị bé dại nhất so với bao quanh mà hàm số rất có thể đạt được. Trong hình học, nó biểu diễn khoảng cách lớn độc nhất vô nhị từ đặc điểm đó sang điểm kia và khoảng tầm cách nhỏ dại nhất từ đặc điểm này sang điểm nọ. Trong toán học tập ta nên định nghĩa rõ ràng hơn về lý thuyết cực trị của một hàm số bất kỳ.
Định nghĩa
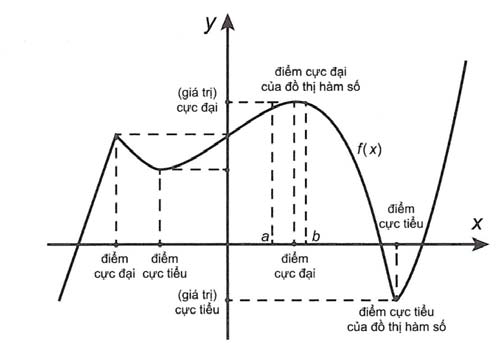
Giả sử hàm số f xác định trên K (K ⊂ ℝ) với x0 ∈ K
a) x0 được hotline là điểm cực đại của hàm số f giả dụ tồn trên một khoảng (a;b) ⊂ K cất điểm x0 làm sao để cho f(x) 0), ∀ x ∈ (a;b) x0
→ khi ấy f(x0) được hotline là giá bán trị cực đại của hàm số f.
b) x0 được gọi là điểm cực đái của hàm số f ví như tồn trên một khoảng (a;b) ⊂ K chứa điểm x0 làm thế nào để cho f(x) > f(x0), ∀ x ∈ (a;b) x0
→ khi ấy f(x0) được gọi là cực hiếm cực tè của hàm số f.
Chú ý:
1) Điểm cực lớn (cực tiểu) x0 được gọi chung là vấn đề cực trị. Giá trị cực đại (cực tiểu) f(x0) của hàm số được gọi tầm thường là cực trị. Hàm số hoàn toàn có thể đạt cực đại hoặc rất tiểu tại nhiều điểm bên trên tập đúng theo K.
2) Nói chung, giá chỉ trị cực lớn (cực tiểu) f(x0) chưa phải là giá bán trị lớn nhất (nhỏ nhất) của hàm số f bên trên tập K; f(x0) chỉ với giá trị lớn số 1 (nhỏ nhất) của hàm số f bên trên một khoảng (a;b) chứa x0.
3) nếu x0 là 1 trong những điểm rất trị của hàm số f thì điểm (x0; f(x0)) được gọi là điểm cực trị của đồ gia dụng thị hàm số f.
Điều kiện đề xuất để hàm số đạt cực trị:
Định lí 1
Giả sử hàm số f đạt cực trị trên điểm x0. Khi đó, nếu như f tất cả đạo hàm trên điểm x0 thì f’(x0) = 0.
Chú ý:
1) Điều ngược lại có thể không đúng. Đạo hàm f’ hoàn toàn có thể bằng 0 trên điểm x0 tuy vậy hàm số f không đạt rất trị tại điểm x0.
2) Hàm số rất có thể đạt cực trị trên một điểm cơ mà tại đó hàm số không tồn tại đạo hàm.
Điều khiếu nại đủ nhằm hàm số đạt cực trị
Định lí 2
a) ví như f’(x) đổi vệt từ âm sang trọng dương khi x đi qua điểm x0 (theo chiều tăng) thì hàm số đạt cực tiểu trên x0.
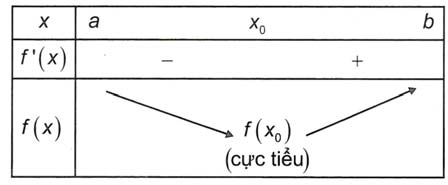
b) nếu f’(x) đổi lốt từ dương thanh lịch âm lúc x trải qua điểm x0 (theo chiều tăng) thì hàm số đạt cực to tại x0.
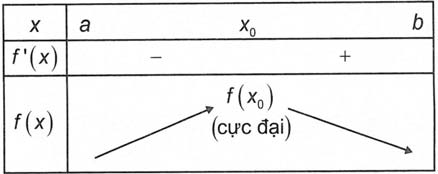
Định lí 3
Giả sử hàm số f tất cả đạo hàm cấp một trên khoảng tầm (a;b) đựng điểm x0, f’(x0) = 0 và f gồm đạo hàm cấp hai khác 0 trên điểm x0.
a) giả dụ f’’(x0) 0.
b) nếu f’’(x0) > 0 thì hàm số f đạt rất tiểu trên điểm x0.
c) ví như f’’(x0) = 0 thì ta chưa thể kết luận được, bắt buộc lập bảng đổi thay thiên hoặc bảng xét vệt đạo hàm.
Phân dạng bài tập
Dạng 1: Tính đạo hàm để tìm rất trị của hàm số y = f(x)
phương thức giảiQuy tắc ITìm tập xác định.Tính y’ = f’(x). Tìm kiếm x lúc f’(x) = 0 hoặc f’(x) ko xác định.Tính những giới hạn nên thiết.Lập bảng phát triển thành thiên.Kết luận những điểm cực trị.Quy tắc IITìm tập xác định.Tính y’ = f’(x). Giải phương trình f’(x) = 0 để tìm những nghiệm x1, x2,… (nếu có) của nó.Tính f’’(x) cùng suy ra f’’(x1), f’’(x2),…Dựa vào vết f’’(x1), f’’(x2),… nhằm kết luận.
Ghi nhớ: phép tắc II không dùng được vào trường vừa lòng f’(x) = 0 vô nghiệm hoặc

Câu 1. đến hàm số y = x4 – 2x2 + 1 tất cả bao nhiêu điểm rất trị?
A. 2
B. 3
C. 1
D. 0
Lời giải
Chọn B
Tập xác định: D = ℝ.
Đạo hàm: y’ = 4x3 – 4x = 4x (x2 – 1)
y’ = 0

Giới hạn:

Bảng thay đổi thiên
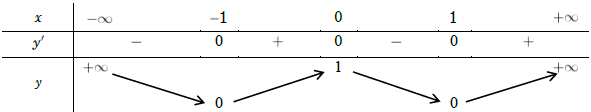
Ta thấy: Hàm số đạt cực tiểu trên x = ±1, giá trị cực tè là y
CT = 0; hàm số đạt cực đại tại x = 0, giá trị cực to là y
CĐ = 1. Cho nên vì vậy hàm số có bố cực trị.
Câu 2. tìm kiếm điểm cực lớn x0 của hàm số y = x3 – 3x +1.
A. X0 = 2
B. X0 = 1
C. X0 = -1
D. X0 = 3
Lời giải
Chọn C
Tập xác định: D = ℝ.
Đạo hàm: y’ = 3x2 – 3
y’ = 0

Giới hạn:

Bảng thay đổi thiên
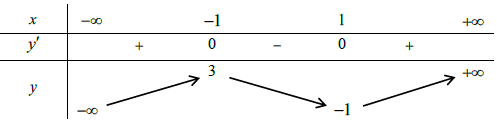
Dựa vào bảng biến chuyển thiên, ta thấy hàm số đạt cực lớn tại x0 = -1.
Câu 3. Hàm số

A. 3
B. 0
C. 2
D. 1
Lời giải
Chọn B
Tập xác định: D = ℝ 2
Ta tất cả

Giới hạn

Bảng đổi mới thiên
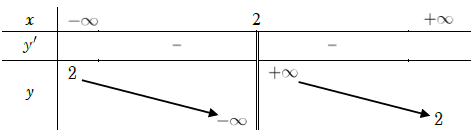
Ta thấy hàm số vẫn cho không tồn tại cực trị.
Dạng 2: Tìm rất trị của hàm số dựa vào bảng đổi mới thiên hoặc đạo hàm (cho sẵn).
một số trong những tính chất nên lưu ýCho hàm số f(x), g(x) cùng tất cả đạo hàm bên trên tập D. Lúc đó:
–
–
–
–
–

– y = f(x)

– Đặt g(x) là hàm số buộc phải xét, ta tính đạo hàm g’(x).
– kết hợp các bề ngoài xét lốt tích, thương, tổng (hiệu) những biểu thức để sở hữu được bảng xét dấu cho g’(x).
– phụ thuộc vào bảng xét dấu giành cho g’(x) để tóm lại về rất trị của hàm số.
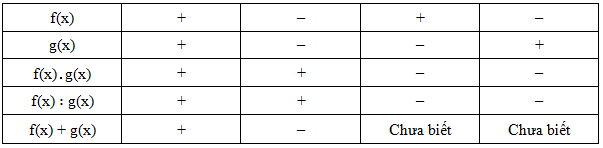
– nhắc lại luật lệ về vết của tích, thương, tổng (hiệu) những biểu thức:
Câu 1. cho hàm số y = f(x) xác định, tiếp tục trên và có bảng biến đổi thiên
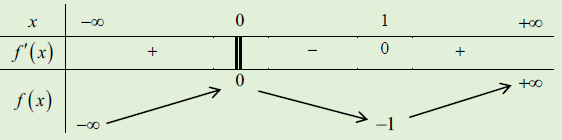
Khẳng định nào sau đó là khẳng định đúng?
A. Hàm số y = f(x) có giá trị cực tiểu bằng 1
B. Hàm số y = f(x) có mức giá trị lớn nhất bằng 0 với giá trị nhỏ dại nhất bởi 1
C. Hàm số y = f(x) đạt cực đại tại x = 0 cùng đạt rất tiểu tại x = 1
D. Hàm số y = f(x) có đúng một cực trị
Lời giải
Chọn C
Dựa vào bảng đổi mới thiên, ta thấy hàm số đạt rất tiểu tại điểm x = 1
Tại x = 0 tuy nhiên đạo hàm f’(x) không tồn tại tuy nhiên hàm số f(x) vẫn khẳng định và thường xuyên nên hàm số đạt cực đại tại x = 0.
Câu 2. mang đến hàm số y = f(x) có bảng biến đổi thiên:
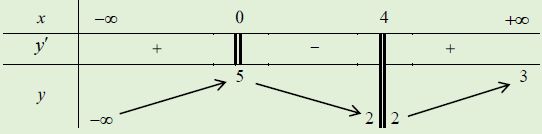
Khẳng định nào dưới đây sai?
A. Hàm số y = f(x) nghịch thay đổi trên khoảng tầm (0;4)
B. Hàm số y = f(x) đạt cực to tại điểm x = 0
C. Hàm số y = f(x) đồng thay đổi trên các khoảng (-∞; 0) và (4; +∞)
D. Hàm số y = f(x) có hai điểm rất trị
Lời giải
Chọn D
Tại x = 0 mặc dù đạo hàm không xác minh nhưng hàm số y = f(x) vẫn xác định và liên tục nên hàm số đạt cực lớn tại x = 0. Trên x = 4 thì hàm số y = f(x) ko xác định, vì chưng vậy hàm số không tồn tại cực trị trên x = 4.
Do đó hàm số chỉ bao gồm duy duy nhất một rất trị.
Câu 3. mang lại đồ thị (C) của hàm số y = f(x) gồm y’ = (1 + x)(x + 2)2(x – 3)3(1 – x2). Trong số mệnh đề sau, tra cứu mệnh đề đúng:
A. (C) bao gồm một điểm rất trị
B. (C) tất cả hai điểm rất trị
C. (C) có tía điểm cực trị
D. (C) có bốn điểm cực trị
Lời giải
Chọn B
Xét đạo hàm: y’ = (1 + x)(x + 2)2(x – 3)3(1 – x2) = (1 + x)2(x + 2)2(x – 3)3(1 – x)
y’ = 0

Vì x = -1, x = -2 là các nghiệm kép của y’ đề xuất y’ không đổi dấu khi qua hai điểm này; x = 1, x = 3 là nghiệm kép của y’ cần y’ đổi vết khi qua những điểm x = 1, x = 3.
Do đó hàm số có hai điểm cực trị x = 1, x = 3.
Cần nhớ: mang đến n là số nguyên dương.
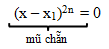
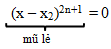
Câu 4. mang lại hàm số y = f(x) gồm đạo hàm trên ℝ và gồm bảng xét vệt f’(x) như sau
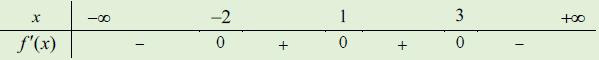
Hỏi hàm số y = f (x2 – 2x) tất cả bao nhiêu điểm cực tiểu?
A. 4
B. 2
C. 3
D. 1
Lời giải
Chọn D
Đặt g(x) = f (x2 – 2x)
Ta bao gồm g’(x) = (2x – 2)․f’(x2 – 2x)
Xét g’(x) ≥ 0 ⇔ (2x – 2)․f’(x2 – 2x) ≥ 0

Hợp nghiệm của (*), (**) ta gồm g’(x) ≥ 0

Do đó g’(x) ≤ 0

Ta tất cả bảng trở nên thiên:
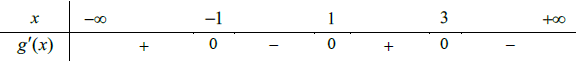
Vậy hàm số y = g(x) = f (x2 – 2x) có đúng 1 điểm cực đái là x = 1.
Câu 5. cho hàm số bậc tư y = f(x). Bảng xét dấu bên dưới là của đạo hàm f’(x). Hàm số gồm bao nhiêu điểm rất trị?
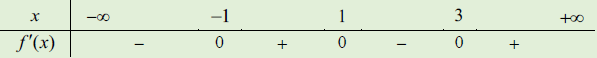
A .1
B. 2
C. 3
D. 4
Lời giải
Chọn C
Ta tất cả

g’(x) = 0

Bảng xét dấu
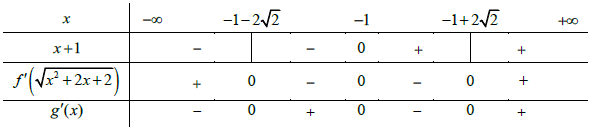
Từ bảng xét dấu ta suy ra hàm số gồm 3 điểm rất trị.
Lưu ý: Để xét lốt g’(x) , ta lựa chọn 1 giá trị x0 thuộc khoảng chừng đang xét rồi núm vào lần lượt những hàm x + 1,

– Để xét vệt g’(x) trên khoảng chừng ta chọn giá trị x0 = 2 ∈ , nỗ lực số 2 vào x + 1, ta được vết dương (+), thế 2 vào ta được


– Để xét vệt g’(x) trên khoảng tầm , ta lựa chọn giá trị x0 = 1 ∈ , thay tiên phong hàng đầu vào x + 1 ta được vệt dương (+), thay tiên phong hàng đầu vào ta được


Câu 6. mang lại hàm số tất cả đồ thị như mẫu vẽ bên. Số điểm cực trị của hàm số đã đến là:
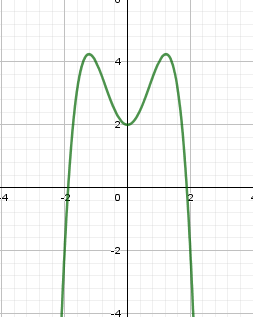
A. 3
B. 1
C. 2
D. 0
Lời giải
Chọn A
Hàm số có ba điểm cực trị.
Câu 7. cho hàm số y = f(x) gồm bảng biến hóa thiên như sau
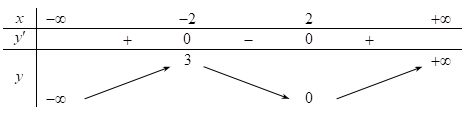
Tìm giá bán trị cực đại y
CĐ và cực hiếm cực tè y
CT của hàm số đang cho.
A. Y
CĐ = 2 cùng y
CT = 0
B. Y
CĐ = 3 với y
CT = 0
C. Y
CĐ = 3 cùng y
CT = -2
D. Y
CĐ = -2 cùng y
CT = 2
Lời giải
Chọn B
Dựa vào bảng đổi thay thiên của hàm số ta gồm y
CĐ = 3 với y
CT = 0
Câu 8. đến hàm số f(x) có bảng thay đổi thiên như sau:
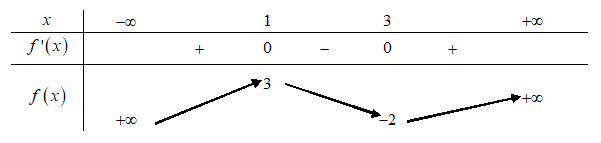
Hàm số đạt cực to tại:
A. X = -2
B. X = 3
C. X = 1
D. X = 2
Lời giải
Chọn C
Hàm số f(x) xác định tại x = 1, f’(1) = 0 với đạo hàm đổi lốt từ (+) lịch sự (–).
Câu 9. mang đến hàm số y = ax4 + bx2 + c (a, b, c ∈ ℝ) bao gồm đồ thị như mẫu vẽ bên.
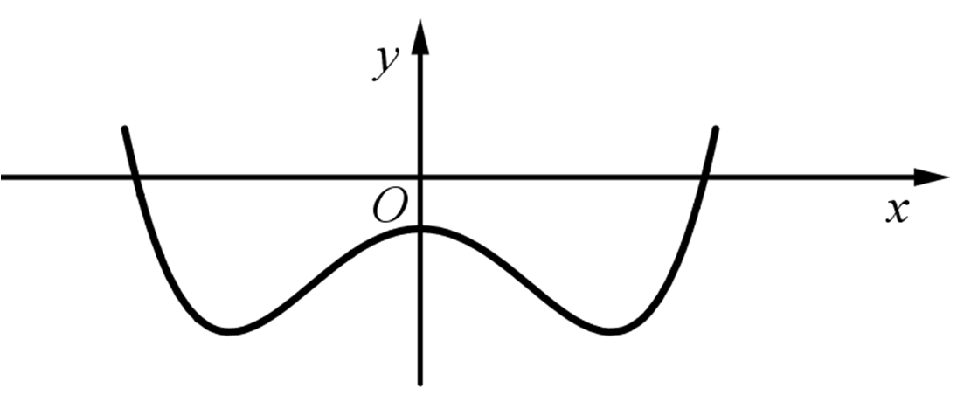
Số điểm cực trị của hàm số đã đến là
A. 3
B. 0
C. 1
D. 2
Lời giải
Chọn A
Dạng 3: tìm tham số vừa lòng điều kiện rất trị của hàm số
phương thức giảiTa có: y = ax3 + bx2 + cx + d (*)
⟶ y’ = 3ax2 + 2bx + c
Điều kiện nhằm hàm số tất cả n cực trị hoặc không tồn tại cực trị.
Ta xét bảng sau (a và ∆ là của đạo hàm y’):

– Hàm số (*) tất cả hai rất trị

– Hàm số (*) có một rất trị

– Hàm số (*) có cực trị

– Hàm số (*) không có cực trị

– Hàm số gồm cực trị tại x = x0
Ta có: y’(x0) = 0. Sau khi kiếm được m thì nuốm ngược quay lại để lập bảng biến chuyển thiên cho hàm số rồi tóm lại nhận hay loại giá trị m này.
– Hàm số đạt cực to tại x = x0 (hoặc hàm số đạt rất tiểu tại x = x0)
Ta có: y’(x0) = 0. Sau khi tìm được m thì cầm cố ngược quay lại để lập bảng đổi thay thiên cho hàm số rồi tóm lại nhận hay một số loại giá trị m này (hoặc rất có thể thay m tìm được vào đạo hàm trung học cơ sở để xét vết xem có cân xứng không).
Đồ thị hàm số bao gồm điểm rất trị là M(x0; y0)
Ta có:

Đồ thị hàm số gồm hai điểm rất trị là A(x
A; y
A), B(x
B; y
B)
Ta có:

Điều kiện cực trị tương quan đến các trục tọa độ:
Đồ thị hàm số có hai điểm rất trị nằm khác phía trục Oy

Đồ thị hàm số có hai điểm rất trị nằm thuộc phía trục Oy

Để ý: Trong điều kiện trên, ta sẽ thay điều kiện

Vì vậy

Ta có đổi khác tương đương tiếp sau đây (phù đúng theo trắc nghiệm):

– Đồ thị hàm số tất cả hai điểm cực trị nằm không giống phía trục Ox

– Đồ thị hàm số bao gồm hai điểm cực trị nằm thuộc phía trục Ox

(trong hai điều kiện trên thì y1, y2 là hai quý giá cực trị của hàm số bậc ba).
– Đồ thị hàm số gồm hai điểm cực trị giải pháp đều trục Ox

– Đồ thị hàm số tất cả hai điểm rất trị phương pháp đều trục Oy

(I là điểm uốn)
Lưu ý: cách tìm điểm uốn nắn I trang bị thị bậc ba y = ax3 + bx2 + cx + d = 0 là: y’ = 3ax2 + 2bx + c, y’’ = 6ax + 2b , cố

I ⇒ I(x
I; y
I).Các phương pháp giải tích liên quan
a) Định lí Vi-ét: đến phương trình ax2 + bx + c = 0 (*) có hai nghiệm x1, x2
Ta có:

b) công thức nghiệm của phương trình ax2 + bx + c = 0 (*)
(*) gồm hai nghiệm minh bạch

(*) có hai nghiệm trái lốt ⇔ ac 1c1 + b2c2 = 0

Khoảng giải pháp từ điểm M (x
M ; y
M ) đến ∆: ax + by + c = 0 là

Đặc biệt: d(M; Ox) = |y
M|, d(M; Oy) = |x
M|
Câu 1. với cái giá trị làm sao của m thì đồ gia dụng thị hàm số y = ⅓x3 + mx2 + (m + 6) x – 2m + 1 có cực đại, cực tiểu.
A. M ∈ (-∞; -3) ∪ (2; +∞)
B. M ∈ (-∞; -3) ∪ (-2; +∞)
C. M ∈ (-∞; -2) ∪ 3; +∞)
D. M ∈ (-∞; 2) ∪ (3; +∞)
Lời giải
Chọn C
Tập xác định : D = ℝ
Đạo hàm: y’ = x2 + 2mx + m + 6
Ta thấy a = 1 ≠ 0. Hàm số tất cả cực đại, rất tiểu ⇔ y’ đổi vết hai lần trên tập xác định
⇔ ∆’ > 0 ⇔ mét vuông – (m + 6) > 0

Câu 2. tra cứu tất những giá trị thực của tham số m để hàm số y = (m + 2) x3 + 3x2 + mx – 6 bao gồm 2 cực trị ?
A. M ∈ (-3;1) 2
B. M ∈ (-3;1)
C. M ∈ (-∞;-3) ∪ (1; +∞)
D. M ∈ <-3;1>Lời giải
Chọn A
Tập khẳng định : D = ℝ
Đạo hàm: y’ = 3(m + 2) x2 + 6x + m
Hàm số bao gồm hai rất trị

Câu 3. Tập hợp tất cả giá trị của m để hàm số y = = ⅓(m – 1) x3 – mx2 + mx – 5 gồm cực trị là:
A.

B. M ≠ 1
C. M > 0
D. M ≥ 0
Lời giải
Chọn C
Tập xác minh : D = ℝ
Đạo hàm: y’ = (m – 1) x2 – 2mx + m
Hàm số sẽ cho tất cả cực trị khi còn chỉ khi


Câu 4. Tìm toàn bộ các quý giá thực của m để hàm số y = x3 – 2x2 + (m + 3) x – 1 không có cực trị?
A.
B.

C.

D.

Lời giải
Chọn A
Tập xác minh : D = ℝ
Đạo hàm: y’ = 3x2 – 4x + m + 3
Ta thấy a = 1 ≠ 0. Vậy hàm số không tồn tại cực trị ⇔ ∆’ ≤ 0
⇔ (-2)2 – 3(m + 3) ≤ 0 ⇔ -3m – 5 ≤ 0 ⇔
Câu 5. giá trị của m để hàm số y = x3 – 3mx2 + 3(m2 – 1) x + m đạt cực lớn tại x = 1 là
A. M = -1
B. M = -2
C. M = 2
D. M = 0
Lời giải
Chọn C
Tập xác định: D = ℝ
Đạo hàm: y’ = 3x2 – 6mx + 3(m2 – 1)
Hàm số có cực to tại x = 1 đề nghị y’(1) = 0 ⇒ 3 – 6m + 3(m2 – 1) = 0 ⇒

Xét m = 0. Ta gồm y’ = 3x2 – 3; y’’ = 6x. Khi ấy y’’(1) = 6 > 0 suy ra hàm số đạt cực tiểu trên x = 1 (loại m = 0 do trái đưa thiết).
Xét m = 2. Ta có y’ = 3x2 – 12x + 9; y’’ = 6x – 12. Khi ấy y’’(1) = -6 3 + x2 + (m2 – 6) x + 1 đạt rất tiểu trên x = 1
A.
B. M = 1
C. M = -4
D. M > – ⅓
Lời giải
Tập xác minh : D = ℝ
Đạo hàm: y’ = 3mx2 + 2x + m2 – 6
Hàm số đạt rất tiểu trên x = 1 ⇒ y’(1) = 0 ⇒ 3m+ 2 + m2 – 6 = 0 ⇒
Xét m = 1. Ta có y’ = 3x2 + 2x – 5; y’’ = 6x + 2. Lúc đó y’’(1) = 8 > 0, hàm số đã cho đạt rất tiểu tại x = 1. Bởi vậy m = 1 thỏa mãn.
Xét m = -4. Ta có y’ = -12x2 + 2x + 10; y’’ = -24x + 2. Lúc đó y’’(1) = -22 3 + bx2 + cx + d (*) cách thức giải
Viết phương trình mặt đường thẳng qua nhị điểm cực trị của trang bị thị y = ax3 + bx2 + cx + d (*):
Giả sử thứ thị hàm số (*) tất cả hai điểm rất trị, ta triển khai theo các cách sau nhằm viết phương trình mặt đường thẳng qua hai điểm cực trị kia :
Phương pháp từ luậnChia f(x) cho f’(x) như sau:
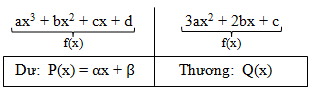
Khi đó, hàm số được viết lại: f(x) = f’(x)․Q(x) + αx + β
Tọa độ các điểm cực trị thỏa H64 hay f(x) = αx + β
Phương pháp Trắc nghiệm– cách viết 1:

– phương pháp viết 2:
Tìm điểm uốn của đồ thị hàm số y = ax3 + bx2 + cx + d (*):
Xét dáng vẻ đồ thị hàm bậc ba bên dưới (đồ thị gồm hai điểm cực trị A, B), nhìn vào vật dụng thị tại ở kề bên điểm A, ta thấy bề lõm của nó hướng xuống (lồi); chú ý vào đồ vật thị tại lân cận điểm B, ta thấy bề lõm của nó hướng lên trên mặt (lõm). Vậy sẽ sở hữu một tinh quái giới đựng đồ thị gửi từ lồi quý phái lõm, tinh ranh giới ấy được gọi là điểm uốn của thứ thị (trong hình là vấn đề I).
– Đặc biệt: Nếu đồ vật thị hàm số gồm hai điểm cực trị là A, B thì I đã là trung điểm của đoạn AB.
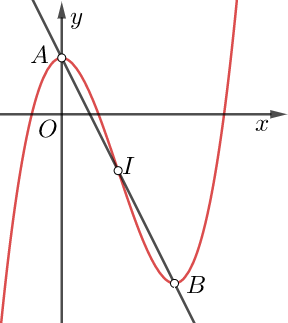
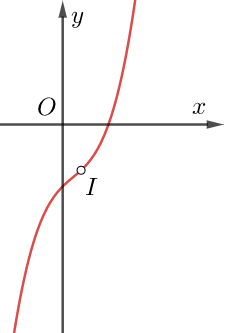
Cách tìm kiếm điểm uốn nắn I:
– bước 1: Tính y’ = 3ax2 + 2bx + c, y’’ = 6ax + 2b
– bước 2: cho y’’ = 6ax + 2b = 0 , cố vào hàm số nhằm y
I . Từ phía trên ta có điểm uốn I(x
I; y
I) của vật thị hàm bậc ba.
Tính chất quan trọng: Điểm uốn nắn I đó là tâm đối xứng của thiết bị thị hàm bậc cha tức là ngẫu nhiên đường thẳng như thế nào qua I nếu cắt đồ thị tại nhì điểm sót lại M, N thì I luôn luôn là trung điểm đoạn MN.
Bài tập vận dụngCâu 1. đến hàm số y = f(x) = x3 – x + m (1). Viết phương trình đường thẳng trải qua hai điểm rất trị của đồ gia dụng thị hàm số (1).
A.

B. Y = -x – m
C.

D.
Đánh giá
Với vấn đề này, xin được trả lời hai phương pháp để bạn đọc chọn lọc phương án về tối ưu đến mình.
– giải pháp giải 1: làm theo lý luận truyền thống.
– giải pháp giải 2: nhờ vào công thức đang cung cấp.
Với bí quyết giải 1, ta triển khai phép phân tách y mang đến y’ trên giấy tờ nháp như sau :

Lời giải
Cách giải 1
Chọn D
Tập xác định : D = ℝ
Đạo hàm: y’ = 3x2 – 1; y’ = 0 bắt buộc hàm số luôn luôn có 2 rất trị.
Hàm số được viết lại

Tọa độ những điểm cực trị của đồ vật thị hàm số luôn thỏa mãn:

Phương trình con đường thẳng qua nhị điểm cực trị của đồ vật thị là
Cách giải 2
Tập xác định: D = ℝ
Đạo hàm: y’ = 3x2 – 1; y’ = 0 đề xuất hàm số luôn có 2 cực trị.
Dựa vào công thức , ta viết phương trình đường thẳng qua nhị điểm cực trị như sau:

Câu 2. cho biết thêm có một tham số m để đồ thị hàm số y = 2x3 + 3(m – 3) x2 + 11 – 3m có hai điểm cực trị, đồng thời hai điểm cực trị đó cùng điểm C(0; -1) trực tiếp hàng. Tìm khẳng định đúng:
A. M ∈ (3; 6)
B. M ∈ (4; 7)
C. M ∈ (1; 4)
D. M ∈ (-1; 2)
Lời giải
Chọn A
Cách giải 1
Chia y đến y’ như sau:

Tập xác định: D = ℝ
Đạo hàm: y’ = 6x2 + 6(m – 3) x
y’ = 0 ⇔ 6x(x + m – 3) = 0 ⇔
Hàm số bao gồm hai rất trị ⇔ 3 – m ≠ 0 ⇔ m ≠ 3
Tọa độ các điểm cực trị của trang bị thị hàm số luôn thỏa mãn :

Điểm C(0; -1) thuộc con đường thẳng qua nhì điểm cực trị cần -1 = 11 – 3m ⇔ m = 4 (thỏa mãn).
Cách giải 2
Tập xác định: D = ℝ
Đạo hàm: y’ = 6x2 + 6(m – 3) x
y’ = 0 ⇔ 6x(x + m – 3) = 0 ⇔
Hàm số tất cả hai rất trị ⇔ 3 – m ≠ 0 ⇔ m ≠ 3
Áp dụng công thức, ta viết phương trình con đường thẳng qua nhị điểm cực trị của thứ thị :

⇔ y = 2x3 + 3(m – 3) x2 + 11 – 3m –
⇔ y = 2x3 + 3(m – 3) x2 + 11 – 3m – <2x3 + 3(m – 3) x2 + (m – 3)2 x>⇔ -(m – 3)2 x + 11 – 3m
Điểm C(0; -1) thuộc mặt đường thẳng qua nhị điểm rất trị yêu cầu -1 = 11 – 3m ⇔ m = 4 (thỏa mãn).
Câu 3. Tìm quý hiếm của tham số m để đồ thị của hàm số y = x3 – 3x2 – mx + 2 có những điểm cực lớn và rất tiểu cách đều đường thẳng y = x – 1.
A.

B. -3
C.

D. 0
Lời giải
Chọn D
Đánh giá bán : Phương trình y’ = 0 ⇔ 3x2 – 6x – m = 0 chẳng thể cho ra nghiệm rất đẹp như ta mong muốn nên những bài xích toán liên quan tọa độ điểm rất trị đều đề xuất đến phương trình đường thẳng trải qua hai điểm rất trị.
Tập khẳng định : D = ℝ
Đạo hàm: y’ =3x2 – 6x – m
Hàm số gồm hai rất trị ⇔ ∆’ > 0 ⇔ 9 + 3m > 0 ⇔ m > -3 (*)
Phương trình con đường thẳng qua nhị điểm cực trị của vật dụng thị là ∆:

Các điểm rất trị cách đều đường thẳng d: y = x – 1
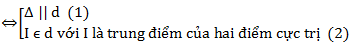
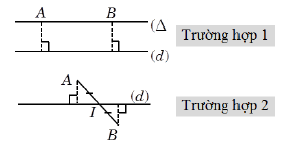
Trường phù hợp 1:

Trường phù hợp 2: điện thoại tư vấn hai điểm cực trị của đồ dùng thị hàm số là

Điểm I là trung điểm của AB nên:


I ∈ d: y = x – 1 ⇔ -m = 1 – 1 ⇔ m = 0 (thỏa mãn vì chưng (*))
Dạng 5: bài toán tìm tham số thỏa mãn điều kiện cực trị hàm số y = ax4 + bx2 + c
phương pháp giảiSố rất trị của hàm số y = ax4 + bx2 + c
Đạo hàm: y’ = 4ax3 + 2bx = 2x (2ax2 + b); y’ = 0

Nhìn vào phương trình y’ = 0, ta thấy luôn có một nghiệm x = 0. Cho nên vì thế việc biện luận tiếp theo sau sẽ nhờ vào vào phương trình (*) . Từ (*) ta thấy:
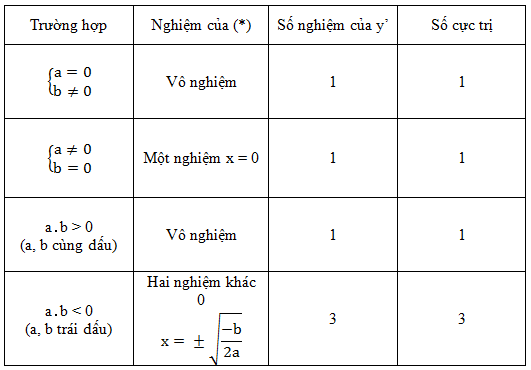
Từ đây, ta có thể khẳng định:
Hàm số không tồn tại cực trị ⇔ a = b = 0
Hàm số tất cả cực trị ⇔ a2 + b2 > 0
Hàm số có một rất trị ⇔

Hàm số có bố cực trị ⇔ a․b 2 + b2 > 0 là biểu đạt a, b không đồng thời bởi 0, tuy nhiên BPT a2 + b2 > 0 mang ý nghĩa phức tạp bởi vì bậc của m có thể ≥ 4. Để khắc phục điều này, ta dùng phương thức phủ định như sau:
Xét


Quay lại giải a2 + b2 > 0 có nghĩa là lấy che định hiệu quả của bước một. Ta bao gồm

Tìm điều kiện để hàm số y = ax4 + bx2 + c thỏa mãn nhu cầu điều khiếu nại K:
– bước 1: Tập xác định: D = ℝ. Đạo hàm: y’ = 4ax3 + 2bx = 2x (2ax2 + b)
y’ = 0 ⇔

– bước 2: Điều khiếu nại hàm số tất cả một cực trị (hoặc có ba cực trị) – xem mục 1 (lý thuyết).
– bước 3: phụ thuộc điều kiện K đề search tham số m rồi đối chiếu điều kiện gồm cực trị (bước 2) trước lúc kết luận.
Xử lý đk K (Công thức trắc nghiệm):
Hàm số gồm cực trị và thỏa mãn:
Hàm số có cực to mà không có cực tiểu

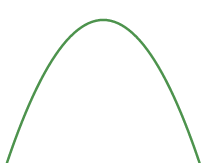
Hàm số bao gồm cực tiểu mà không có cực to

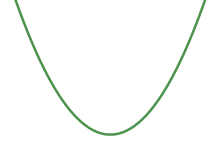
Ba rất trị tạo thành thành tam giác vuông hoặc đều, ta dùng cách làm nhanh

Ba cực trị sinh sản thành tam giác vuông

Ba cực trị tạo ra thành tam giác hầu như

Ba cực trị sinh sản thành tam giác có diện tích s S.

Ta dùng bí quyết nhanh bình phương diện tích s:

Tọa độ bố điểm cực trị của vật thị là A(0;c),

Tam giác ABC gồm

Công thức diện tích khác:

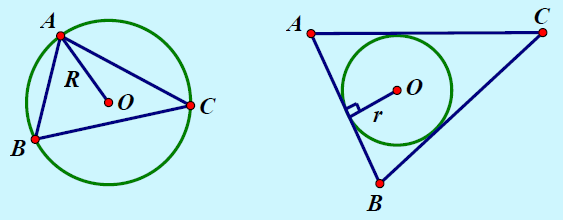
R, r theo đồ vật tự là bán kính đường tròn nước ngoài tiếp và nội tiếp của tam giác
a, b, c là độ dài ba cạnh;

Câu 1. Có tất cả bao nhiêu cực hiếm nguyên của m bên trên miền <-10;10> để hàm số y = x4 – 2(2m + 1) x2 + 7 có cha điểm rất trị?
A. 20
B. 10
C. Vô số
D. 11.
Lời giải
Chọn D
Cách 1: trường đoản cú luận
Tập xác định: D = ℝ .
Ta gồm y’ = 4x3 – 4(2m + 1) x
y’ = 0 ⇔ 4x3 – 4(2m + 1) x = 0

Hàm số đã đến có ba điểm cực trị khi và chỉ khi phương trình y’ = 0 có cha nghiệm phân biệt
⇔ Phương trình (*) bao gồm hai nghiệm tách biệt khác 0 ⇔ 2m + 1 > 0 ⇔ m > -½ .
Vì m nguyên nằm trong <-10;10> yêu cầu m ∈ 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10
Cách 2: Trắc nghiệm
Hàm số có cha cực trị khi và chỉ khi a․b 0 ⇔ m > -½.
Câu 2. Tìm tất cả giá trị của thông số m nhằm hàm số y = mx4 + (m2 – 9) x2 + 10 tất cả 3 cực trị.
A. M ∈ (0; 3)
B. M ∈ (3; +∞)
C. M ∈ (-∞; -3) ∪ (0; 3)
D. M ∈ (-3; 0) ∪ (3; +∞)
Lời giải
Chọn C
Cách 1: trường đoản cú luận
Tập xác định: D = ℝ .
Ta có y’ = 4mx3 – 2(m2 – 9) x = 2x (2mx2 + m2 – 9)
y’ = 0 ⇔

Hàm số đang cho gồm 3 cực trị ⇔ y’ = 0 có 3 nghiệm biệt lập ⇔ Phương trình (1) gồm hai nghiệm riêng biệt khác 0 .

Suy ra m ∈ (-∞; -3) ∪ (0; 3)
Cách 2: Trắc nghiệm
Hàm số có cha cực trị khi và chỉ khi ab 2 – 9) 4 + (m – 1) x2 + 1 – 2m chỉ gồm một rất trị.
A. M ≥ 1
B. M ≤ 0
C. 0 ≤ m ≤ 1
D. M ≤ 0 hoặc m ≥ 1
Lời giải
Chọn D
Hàm số tất cả một cực trị khi còn chỉ khi

⇔ m ≤ 0 ∨ m ≥ 1
Vậy m m ≤ 0 hoặc m ≥ 1 vừa lòng đề bài
Câu 4. Tìm toàn bộ các cực hiếm của tham số m để hàm số

A. M ≥ 0
B. M ≤ 0
C. M ≥ 1
D. M = -1
Lời giải
Chọn B
Nhận xét : bao gồm hai ngôi trường hợp để hàm số y = ax4 + bx2 + c có cực tè mà không tồn tại cực đại:
Một là: Hàm bậc bốn gồm đúng một rất trị và là rất tiểu, lúc đó:

Hai là: Hàm số biến hóa hàm bậc nhị (đồ thị parabol bao gồm bề lõm phía lên), ta có:

Ta thấy

Vậy m ≤ 0 thỏa mãn đề bài.
Câu 5. Tìm tất cả các quý giá của m nhằm hàm số y = (m2 – 1) x4 + mx2 + m – 2 chỉ tất cả một điểm cực lớn mà không tồn tại điểm rất tiểu.
A. -1,5 cách thức giải
Hàm số phân thức bậc nhì trên bậc một
Hàm số:

Tập xác định: D = ℝ

Đạo hàm:


Hàm số có hai điểm cực trị ⇔ y’ đổi vệt hai lần bên trên tập xác định ⇔ g(x) = 0 tất cả hai nghiệm phân minh khác

Đường thẳng đi qua hai điểm cực trị của vật thị có phương trình:

Hàm số y = |f(x)|
Đạo hàm:

Cho trước vật dụng thị hàm số y = f(x) liên tục trên D. Ta xác định đồ thị hàm y = |f(x)|:
– cách 1: giữ nguyên phần trang bị thị y = f(x) nằm phía bên trên trục hoành.
– cách 2: rước đối xứng phần đồ vật thị y = f(x) nằm dưới trục hoành qua trục hoành.
Hợp của nhì phần trên (bỏ phần bên dưới trục hoành), ta được thứ thị hàm y = |f(x)|.
Minh họa:
Đồ thị y = f(x)
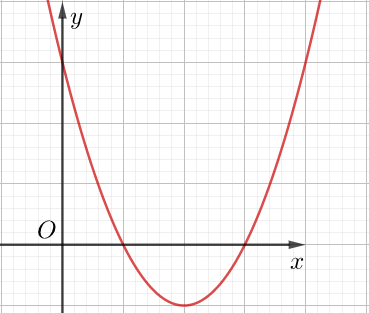
Đồ thị y = |f(x)|
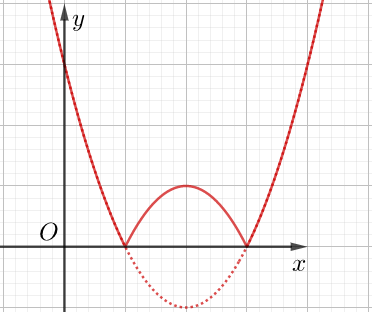
Đúc kết :
Số cực trị hàm y = |f(x)| = số cực trị hàm y = f(x) + Số giao điểm (không tính tiếp xúc)

Hàm số y = f(|x|):
Cho trước thiết bị thị hàm số y = f(x) tiếp tục trên D. Ta xác định đồ thị hàm y = f(|x|)
– bước 1: không thay đổi phần vật dụng thị y = f(x) nằm cạnh phải trục tung (ứng với x ≥ 0); loại bỏ đi phần trang bị thị y = f(x) nằm cạnh trái trục tung (ứng cùng với x bài tập vận dụng
Câu 1. Tìm toàn bộ giá trị tham số m làm sao cho hàm số

A. M ∈ ℝ
B. M = 0
C. M = 1
D. M = -1
Lời giải
Chọn A
Tập xác định: D = ℝ m.
Đạo hàm:

Hàm số có cực đại, rất tiểu ⇔ y’ đổi lốt hai lần trên tập xác định ⇔ g(x) = 0 tất cả hai nghiệm rành mạch khác m

Câu 2. Tìm tất cả giá trị tham số m để điểm A(1; -3) cùng rất hai điểm rất trị của vật dụng thị hàm số

A.
B. M ≠ 1
C.

D.

Lời giải
Chọn C
Tập xác định: D = ℝ -1.
Đạo hàm:

Hàm số tất cả hai cực trị ⇔ y’ đổi dấu hai lần bên trên tập xác định ⇔ g(x) = 0 gồm hai nghiệm rõ ràng khác -1

Phương trình mặt đường thẳng qua nhì điểm rất trị của đồ gia dụng thị là d:

Điểm A(1; -3) ∉ d ⇔ -3 ≠ 2․1 + 2m ⇔
Vậy m CĐ = -2 – m = 7 ⇔ m = -9
Tài liệu về cực trị hàm số
Tổng hợp phần đông tài liệu hay độc nhất cho chăm đề cực trị của hàm số và các vấn đề liên quan. Những tài liệu hầu như được tinh lọc kĩ càng trước khi đăng tải.
1. Bài bác tập cực trị của hàm số
Thông tin tài liệu| Thông tin tài liệu | |
| Tác giả | Thầy Diệp Tuân |
| Số trang | 126 |
| Lời giải bỏ ra tiết | Không |
– triết lý cực trị của hàm số
– Dạng 1: Tìm các điểm rất trị của hàm số.
– Dạng 2: Định tham số m nhằm hàm số f (x) đạt cực trị.
– Dạng 3: Ứng dụng rất trị giải phương trình, bất phương trình, hệ phương trình đại số.
Đồ thị hàm số mũ với logarit là phần kiến thức và kỹ năng rất quan trọng đặc biệt trong lịch trình học lớp 12. Để thành thạo bí quyết vẽ đồ vật thị hàm mũ cùng logarit, các em hãy thuộc eivonline.edu.vn ôn tập kim chỉ nan và xử lý từng cách làm việc dạng này nhé!
Trước khi đi vào từng phần triết lý về thiết bị thị của hàm số mũ và logarit, eivonline.edu.vn vẫn điểm lại cho những em kim chỉ nan về hàm số mũ cùng hàm số logarit trong lịch trình Toán lớp 12 một cách bao quát và ngăn nắp nhất, bởi vì khi bọn họ nắm vững định hướng thì mới hoàn toàn có thể làm bài xích tập trang bị thị bao gồm xác, hiểu bản chất và sớm nhất được.

Chi tiết hơn, eivonline.edu.vn gửi tặng các em cỗ tài liệu full lý thuyết về hàm số nón - hàm số logarit nói tầm thường và dạng toán trang bị thị hàm số mũ và logarit. Những em nhớ sở hữu về nhằm tiện mang lại ôn tập nhé!
Đặc biệt, ở cuối bài viết này sẽ có một tệp tin tổng hợp cục bộ lý thuyết về hàm số luỹ thừa - logarit - hàm mũ với không thiếu thốn công thức, đặc thù và hơn hết là công việc giảiđồ thị hàm số mũ và logarit.
Xem thêm: Con Gái Lai Hàn Của Lâm Chấn Khang Ngày Càng Lém Lỉnh, Thích Mẹ Kim Jun See Làm Điệu
các em nhớ hiểu hết nội dung bài viết để lấy bộ tài liệu này nhé!

1. Ôn lại kim chỉ nan về hàm số cùng đồ thị hàm số mũ với logarit
1.1. Kim chỉ nan về hàm số mũ
1.1.1 Điểm nhanh kiến thức về luỹ thừa và các tính chất liên quan mang lại hàm số mũBởi bởi vì định nghĩa, đặc thù của luỹ thừa có tương quan trực tiếp nối hàm số mũ, tuyệt nói bí quyết khác, hàm số mũ thuộc phạm trù của luỹ thừa (luỹ thừa cải tiến và phát triển được thành 2 dạng hàm số đó là hàm số luỹ thừa với hàm số mũ). đến nên trước khi đi vào chi tiết về hàm số mũ, ta bắt buộc ôn lại kiến thức và kỹ năng về luỹ thừa để vận dụng thật tốt.
Định nghĩa của luỹ thừa