Tìm giá trị lớn nhất, nhỏ nhất của một biểu thức lớp 8
B. Các bài tập tìm giá trị lớn nhất, giá trị nhỏ nhất của một biểu thứcTìm giá trị lớn nhất, nhỏ nhất của một biểu thức là dạng bài tập thường xuất hiện trong các bài kiểm tra môn Toán lớp 8. Trong tài liệu dưới đây, Vn
Doc gửi tới các bạn lý thuyết và một số dạng toán tìm giá trị lớn nhất và nhỏ nhất của biểu thức (biểu thức chứa dấu căn, biểu thức chứa dấu giá trị tuyệt đối,...) giúp các em ôn lại khái niệm cũng như phương pháp tìm giá trị lớn nhất và nhỏ nhất. Mời các em tham khảo chi tiết sau đây.
Bạn đang xem: Cách tìm giá trị nhỏ nhất
A. Giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức
1. Khái niệm
- Nếu với mọi giá trị của biến thuộc một khoảng xác định nào đó mà giá trị của biểu thức A luôn luôn lớn hơn hoặc bằng (nhỏ hơn hoặc bằng) một hằng số k và tồn tại một giá trị của biến để A có giá trị bằng k thì k gọi là giá trị nhỏ nhất (giá trị lớn nhất) của biểu thức A ứng với các giá trị của biến thuộc khoảng xác định nói trên.
2. Phương pháp
a) Để tìm giá trị nhỏ nhất của A, ta cần:
+ Chứng minh A ≥ k với k là hằng số
+ Chỉ ra dấu “=” có thể xảy ra với giá trị nào đó của biến
b) Để tìm giá trị lớn nhất của A, ta cần:
+ Chứng minh A ≤ k với k là hằng số
+ Chỉ ra dấu “=” có thể xảy ra với giá trị nào đó của biến
Kí hiệu: min A là giá trị nhỏ nhất của A; max A là giá trị lớn nhất của A
B. Các bài tập tìm giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức
I. Dạng 1: Tam thức bậc hai
Phương pháp: Đối với dạng tam thức bậc hai ta đưa biểu thức đã cho về dạng bình phương một tổng (hoặc hiệu) cộng (hoặc trừ) đi một số tự do. Tổng quát: d - (a ± b)2 ≤ d Ta tìm được giá trị lớn nhất(a ± b)2± c ≥ ± c Ta tìm được giá trị nhỏ nhất |
Ví dụ 1: Tìm giá trị lớn nhất của biểu thức B = 6 - 8x - x2
Lời giải
Ta có:
B = 6 - 8x - x2 = -(x2 + 8x) + 6
= -(x2 + 8x + 16) + 6 + 16
= -(x + 4)2 + 22
Vì (x +4)2 ≥ 0 ⇒ -(x +4)2 ≤ 0 ⇒ -(x +4)2 + 22 ≤ 22
Do đó, giá trị lớn nhất của biểu thức B là 22
Ví dụ 2. Tìm giá trị nhỏ nhất của biểu thức C = 4x2 + 8x + 10
Lời giải
C = 4x2 + 8x + 10 = (2x)2 + 2.2x.2 + 4 + 6
= (2x + 2)2 + 6
Với mọi x ta có: (2x + 2)2 ≥ 0 ⇒ (2x + 2)2 + 6 ≥ 6
Do đó, giá trị nhỏ nhất của biểu thức C là 6
Ví dụ 3:
a, Tìm giá trị nhỏ nhất của A = 2x2 - 8x + 1
b, Tìm giá trị lớn nhất của B = -5x2 - 4x + 1
Lời giải:
a, A = 2(x2 - 4x + 4) - 7 = 2(x - 2)2 - 7 ≥ -7
min A = -7 khi và chỉ khi x = 2
b,

max

Ví dụ 4: Cho tam thức bậc hai P(x) = ax2 + bx + c
a, Tìm min P nếu a > 0
b, Tìm max P nếu a 0 thì

b, Nếu a
II. Dạng 2: Đa thức có dấu giá trị tuyệt đối
Phương pháp: Có hai cách để giải bài toán này: Cách 1: Dựa vào tính chất |x| ≥ 0. Ta biến đổi biểu thức A đã cho về dạng A ≥ a (với a là số đã biết) để suy ra giá trị nhỏ nhất của A là a hoặc biến đổi về dạng A ≤ b (với b là số đã biết) từ đó suy ra giá trị lớn nhất của A là b. Cách 2: Dựa vào biểu thức chứa hai hạng tử là hai biểu thức trong dấu giá trị tuyệt đối. Ta sẽ sử dụng tính chất: ∀x, y ∈    |
Ví dụ 1: Tìm giá trị nhỏ nhất của các biểu thức sau:
a. A = (3x - 1)2 - 4|3x - 1| + 5
b. B = |x - 2| + |x - 3|
Lời giải:
a,

Đặt

min A = 1

b,



Ví dụ 2: Tìm giá trị nhỏ nhất của C = |x2 - x + 1| + |x2 - x - 2|
Hướng dẫn giải
Ta có:
C = |x2 - x + 1| + |x2 - x - 2| ≥ |x2 - x + 1 + 2 + x - x2| = 3
Min
C = 3 ⇔ (x2 - x + 1)(2 + x - x2) ≥ 0 ⇔ (x + 1)(x - 2) ≤ 0 ⇔ -1 ≤ x ≤ 2
Ví dụ 3: Tìm giá trị nhỏ nhất của T = |x - 1| + |x - 2| + |x - 3| + |x - 4|
Hướng dẫn giải
Ta có |x - 1| + |x - 4| ≥ |x - 1 + 4 - x| = 3 (1)
Và |x - 2| + |x - 3| ≥ |x - 2 +3 - x| = 1(2)
Vậy T ≥ 1 + 3 = 4
Từ (1) suy ra dấu bằng xảy ra khi 1 ≤ x ≤ 4
Từ (2) suy ra dấu bằng xảy ra khi 2 ≤ x ≤ 3
Vậy T có giá trị nhỏ nhất bằng 4 khi 2 ≤ x ≤ 3
Bài tập vận dụng: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức dưới đây:
A = |x - 2004| + |x - 2005|
B = |x - 2| + |x - 9| + 1945
C = -|x - 7| - |y + 13| + 1945
III. Dạng 3: Đa thức bậc cao
Dạng phân thứcPhân thức có tử là hằng số, mẫu là tam thức bậc hai
Các phân thức có dạng khác
Ví dụ 1: Tìm giá trị nhỏ nhất của các đa thức sau:
a. A = x(x - 3)(x - 4)(x - 7)
b. B = 2x2 + y2 - 2xy - 2x + 3
c. C = x2 + xy + y2 - 3x - 3
Lời giải:
a, A = x(x - 3)(x - 4)(x - 7) = (x2 - 7x)(x2 - 7x + 12)
Đặt y = x2 - 7x + 6 thì A = (y - 6)(y + 6) = y2 - 36 ≥ -36
Min

b, B = 2x2 + y2 - 2xy - 2x + 3 = (x2 - 2xy + y2) + (x2 - 2x + 1) + 2

c, C = x2 + xy + y2 - 3x - 3 = x2 - 2x + y2 - 2y + xy - x - y
Ta có




Vậy Min(C + 3) = 0 hay min C = -3⇔ a = b = 0 ⇔ x = y = 1
C. Bài tập vận dụng
1. Bài tập trắc nghiệm
Câu 1. Tìm giá trị lớn nhất của biểu thức B = 10 - x2
A.0 B.10 C. -10 D. 9
Đáp án
Ta có:
Do đó, giá trị lớn nhất của biểu thức B là 10
Chọn B.
Câu 2. Tìm giá trị lớn nhất của biểu thức A = 4x - 2x2
A.0
B. 1
C. 4
D. 2
Đáp án
Ta có;
A = 4x - 2x2 = -2(x2 - 2x)
= -2(x2 - 2x + 1) + 2 = -2(x - 1)2 + 2
Vì
Do đó, giá trị lớn nhất của biểu thức A là 2.
Chọn D.
Câu 3 . Tìm giá trị lớn nhất của biểu thức C = 4x + 3 - x2
A.7
B. 4
C. 3
D. -1
Đáp án
Ta có:
Vì
Do đó, giá trị lớn nhất của C là 7.
Chọn A.
Câu 4. Tìm giá trị lớn nhất của biểu thức D = -x2 + 6x - 11
A.-11 B. 6 C. -2 D. 9
Đáp án
D = -x2 + 6x - 11 = -(x2 - 6x) - 11
= -(x2 - 6x + 9) + 9 - 11
= -(x - 3)2 - 2
Vì
Giá trị lớn nhất của biểu thức D là – 2
Chọn C
Câu 5. Tìm giá trị lớn nhất của biểu thức E = 4x - x2 + 1
A.1 B. 5 C. 3 D. 6
Đáp án
Ta có:
E = 4x - x2 + 1 = -(x2 - 4x) + 1
= -(x2 - 4x + 4) + 4 + 1
= -(x - 2)2 + 5
Vì
Do đó, giá trị lớn nhất của biểu thức E là 5.
Chọn B.
Câu 6. Tìm giá trị nhỏ nhất của biểu thức A = 2x2 + 8x + 11
A.3 B. 8 C. 11 D. 9
Đáp án
Ta có:
A = 2x2 + 8x + 11 = 2(x2 + 4x) + 11
= 2(x2 + 4x + 4) - 8 + 11
= 2(x + 2)2 + 3
Vì
Vậy giá trị nhỏ nhất của biểu thức A là 3
Chọn A.
Câu 7. Tìm giá trị nhỏ nhất của biểu thức E = x2 - 2x + y2 + 4y + 10
A.1 B. 10 C. 5 D. 8
Đáp án
Ta có:
E = x2 - 2x + y2 + 4y + 10
= (x2 - 2x + 1) + (y2 + 4y + 4) + 5
= (x - 1)2 + (y + 2)2 + 5
Vì
Do đó, giá trị nhỏ nhất của E là 5.
Chọn C.
Câu 8. Tìm giá trị nhỏ nhất của biểu thức D = 4x2 + y2 + 6y + 20
A. 20 B. 11 C. 10 D. 16
Đáp án
Ta có;
D = 4x2 + y2 + 6y + 20 = 4x2 + (y2 + 6y + 9) + 11
= 4x2 + (y + 3)2 + 11
Vì:
Suy ra:
Vậy giá trị nhỏ nhất của D là 11
Chọn B.
Câu 9. Tìm giá trị nhỏ nhất của biểu thức G = x2 + 5y2 - 4xy - 8y + 28
A.10 B. 8 C. 20 D. 15
Đáp án
Ta có:
G = x2 + 5y2 - 4xy - 8y + 28
G = (x2 - 4xy + 4y2) + (y2 - 8y + 16) + 8
= (x - 2y)2 + (y - 4)2 + 8
Vì
Suy ra:
Vậy giá trị nhỏ nhất của G là 8.
Chọn B.
2. Bài tập tự luận:
Bài tập 1: Tìm giá trị nhỏ nhất của biểu thức:
a,

b,

c,

d,

Bài tập 2: Tìm giá trị lớn nhất của biểu thức:

--------------------------------
Ngoài ra, Vn
Trên đây, Vn
Doc đã gửi tới các bạn tài liệu Tìm giá trị lớn nhất, nhỏ nhất của một biểu thức. Hy vọng thông qua tài liệu này, các em học sinh sẽ nắm được những dạng toán cơ bản về tìm giá trị lớn nhất và nhỏ nhất của biểu thức. Để làm tốt hơn phần này, các em cần luyện giải nhiều dạng bài tập khác nhau nữa nhé. Chúc các em học tốt.
Ngoài tài liệu trên, mời các em tham khảo thêm đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 các môn Toán 8, Văn 8, Anh 8, Hóa 8... được cập nhật liên tục trên Vn
Doc. Với đề thi học kì 2 lớp 8 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt.
Mời bạn đọc tham khảo thêm một số bài học bổ trợ liên quan:
Toán 8 từ năm học 2023 - 2024 trở đi sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Việc lựa chọn giảng dạy bộ sách nào sẽ tùy thuộc vào các trường. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, Vn
Doc sẽ cung cấp lời giải bài tập sách giáo khoa, sách bài tập, trắc nghiệm toán từng bài và các tài liệu giảng dạy, học tập khác. Mời các bạn tham khảo qua đường link bên dưới:
Tìm giá tị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của biểu thức (biểu thức chứa dấu căn, biểu thức chứa dấu giá trị tuyệt đối,...) là một trong những dạng toán lớp 9 có nhiều bài tương đối khó và đòi hỏi kiến thức vận dụng linh hoạt trong mỗi bài toán.
Bài viết này sẽ chia sẻ với các em một số cách tìm giá trị lớn nhất (GTLN, Max) và giá trị nhỏ nhất (GTNN, Min) của biểu thức (biểu thức đại số chứa dấu căn, chứa dấu giá trị tuyệt đối,...) qua một số bài tập minh họa cụ thể.
* Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức đại số:
* Phương pháp: (đối với biểu thức 1 biến số)
- Muốn tìm giá trị lớn nhất hay giá trị nhỏ nhất của một biểu thức ta có thể biến đổi biểu thức thành dạng: A2(x) + const ;(A biểu thức theo x, const = hằng số).
* Ví dụ 1: Cho biểu thức: A = x2 + 2x - 3.
Tìm GTNN của A.
° Lời giải:
- Ta có: A = x2 + 2x - 3 = x2 + 2x + 1 - 1 - 3 = (x + 1)2 - 4
- Vì (x + 1)2 ≥ 0 ⇒ (x + 1)2 - 4 ≥ -4
⇒ A ≥ - 4 dấu bằng xảy ra, tức A = - 4 ⇔ x + 1 = 0 ⇔ x = -1
- Kết luận: Amin = -4 khi và chỉ khi x = -1.
* Ví dụ 2: Cho biểu thức: A = -x2 + 6x - 5.
Tìm GTLN của A.
° Lời giải:
- Ta có: A = -x2 + 6x - 5 = -x2 + 6x - 9 + 9 - 5 = -(x - 3)2 + 4 = 4 - (x - 3)2
- Vì (x - 3)2 ≥ 0 ⇒ -(x - 3)2 ≤ 0 ⇒ 4 - (x - 3)2 ≤ 4
⇒ A ≤ 4 dấu bằng xảy ra, tức A = 4 ⇔ x - 3 = 0 ⇔ x = 3
- Kết luận: Amax = 4 khi và chỉ khi x = 3.
* Ví dụ 3: Cho biểu thức:
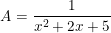
- Tìm x để Amax; tính Amax =?
° Lời giải:
- Để A đạt gía trị lớn nhất thì biểu thức (x2 + 2x + 5) đạt giá trị nhỏ nhất.
- Ta có: x2 + 2x + 5 = x2 + 2x + 1 + 4 = (x + 1)2 + 4
- Vì (x + 1)2 ≥ 0 nên (x + 1)2 + 4 ≥ 4
dấu "=" xảy ra khi và chỉ khi x + 1 = 0 ⇔ x = -1
Vậy
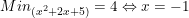
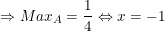

* Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức chứa dấu căn:
* Phương pháp: (đối với biểu thức 1 biến số)
- Cũng tương tự như cách tìm ở phương pháp trên, vận dụng tính chất của biểu thức không âm như:
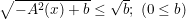
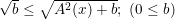
- Dấu "=" xảy ra khi A = 0.
* Ví dụ 1: Tìm GTNN của biểu thức:
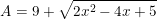
° Lời giải:
- Ta thấy:
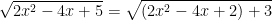
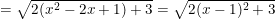
Vì (x - 1)2 ≥ 0 ⇒ 2(x - 1)2 ≥ 0 ⇒ 2(x - 1)2 + 3 ≥ 3
nên
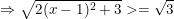
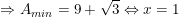
* Ví dụ 2: Tìm GTLN của biểu thức:
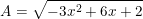
° Lời giải:
- Ta có:
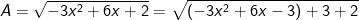
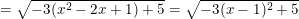
Vì (x - 1)2 ≥ 0 ⇒ -3(x - 1)2 ≤ 0 ⇒ -3(x - 1)2 + 5 ≤ 5
nên
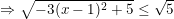
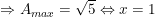
* Ví dụ 3: Tìm GTLN của biểu thức:
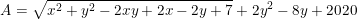
° Lời giải:
- Ta có:
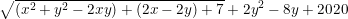
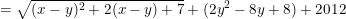
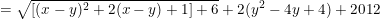
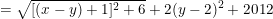
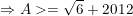
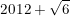
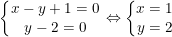
* Ví dụ 4: Tìm GTLN của biểu thức:
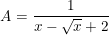
° Lời giải:
- Điều kiện: x≥0
- Để A đạt giá trị lớn nhất thì
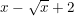
- Ta có:
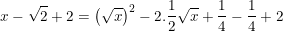
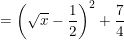
Lại có:
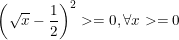
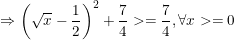
Dấu"=" xảy ra khi
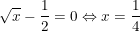
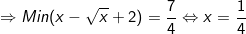
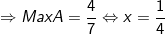
- Kết luận: GTLN của A = 4/7 khi x = 1/4.
* Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức chứa dấu giá trị tuyệt đối:
* Phương pháp: (đối với biểu thức 1 biến số)
- Bài toán này cũng chủ yếu dựa vào tính không âm của trị tuyệt đối.
* Ví dụ 1: Tìm GTLN của biểu thức:
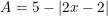
° Lời giải:
- Ta có: |2x - 2| ≥ 0 ⇔ -|2x - 2| ≤ 0 ⇔ 5 -|2x - 2| ≤ 5
Dấu "=" xảy ra khi |2x - 2| = 0 ⇔ 2x - 2 = 0 ⇔ x = 1
Vậy Amax = 5 ⇔ x = 1
* Ví dụ 2: Tìm GTNN của biểu thức: A = |9 - x| - 3
° Lời giải:
- Ta có: |9 - x| ≥ 0 ⇔ |9 - x| ≥ 0 ⇔ |9 - x| - 3 ≥ -3
Dấu "=" xảy ra khi |9 - x| = 0 ⇔ 9 - x = 0 ⇔ x = 9
Vậy Amin = -3 ⇔ x = 9
Như vậy, các bài toán trên dựa trên các biến đổi về dạng tổng hoặc hiệu của biểu thức không âm (bình phương, trị tuyệt đối,...) và hằng số để tìm ra lời giải.
Thực tế, còn nhiều bài toán phải sử dụng bất đẳng thức Cauchy (Cosi) cho hai số a, b không âm:
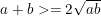
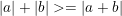
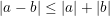
* Ví dụ 1: Tìm giá trị nhỏ nhất (GTNN) của biểu thức:
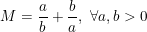
° Lời giải:
- Vì a,b>0 nên
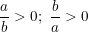
- Áp dụng bất đẳng thức Cauchy (còn gọi là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân AM-GM (Arithmetic Means - Geometric Means)).
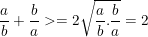
Dấu "=" xảy ra khi
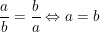
- Kết luận: Giá trị nhỏ nhất của M = 2 ⇔ a = b.
* Ví dụ 2: Tìm giá trị nhỏ nhất (GTNN) của biểu thức:
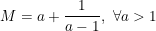
° Lời giải:
- Vì a > 1 nên a - 1 > 0 ta có:
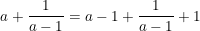
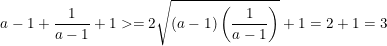
Dấu "=" xảy ra khi
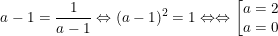
Đối chiếu điều kiện a > 1 nên chỉ nhận a = 2; loại a = 0.
- Kết luận: GTNN của M = 3 ⇔ a = 2.
Hy vọng với bài viết Cách tìm giá trị lớn nhất (GTLN, Max) và giá trị nhỏ nhất (GTNN, Min) của biểu thức ở trên giúp các em hiểu rõ hơn về dạng toán này.
Xem thêm: Những nội dung cơ bản của thông tư 08/2013 của thanh tra chính phủ
Việc vận dụng vào mỗi bài toán đòi hỏi kỹ năng làm toán của các em, kỹ năng này có được khi các em chịu khó rèn luyện qua nhiều bài tập. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để
