Một Kỹ Sư Cơ Khí Đã Biến Tam Giác Bất Khả Thi 'Penrose'?

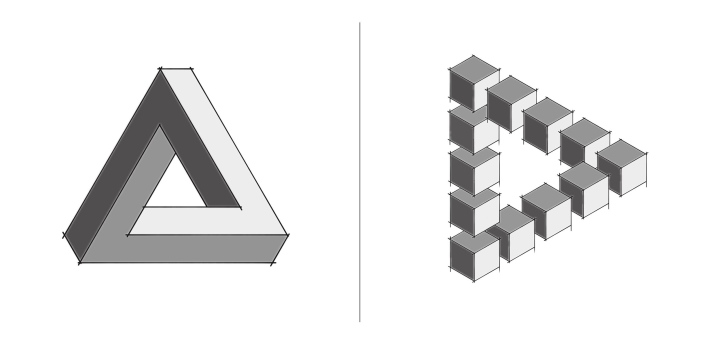
Tam giác Penrose được gọi là \"Vật thể bất khả thi\" bởi vì đó là một hình tam giác bất khả thi, có nghĩa là nó không thể tồn tại trong không gian ba chiều được. Điều này có nghĩa là mặc dù trong không gian hai chiều, ta có thể vẽ Tam giác Penrose một cách dễ dàng, nhưng không thể xây dựng hoặc làm thật như một vật thể trong không gian ba chiều. Tam giác Penrose được tạo ra bởi nhà toán học và nhà vật lý người Anh Roger Penrose và nó đã trở thành một hình ảnh phổ biến trong nghệ thuật và thiết kế và được sử dụng để tạo ra hiệu ứng ngộ nghĩnh và huyền ảo.

Tam giác Penrose được tạo ra bởi nhà toán học người Anh Roger Penrose vào năm 1958.

Tam giác Penrose có 2 loại chính, đó là Penrose tribar và Penrose tiling. - Penrose tribar là một hình tam giác bất khả thi, có cấu trúc giống với một chiếc xúc xắc được bẻ gập lại. Nó được tạo ra lần đầu tiên bởi nhà toán học Roger Penrose vào năm 1958 và được coi là biểu tượng của sự bất khả thi trong toán học.- Penrose tiling là một mẫu lặp lại vô hạn của các hình bình hành và hình ngũ giác, có tính chất tự tạo và đối xứng đa dạng. Nó được cũng cấp bởi Roger Penrose vào năm 1974 và được sử dụng trong nhiều lĩnh vực như nghệ thuật, kiến trúc và vật lý. Tuy nhiên, cả hai loại đều có chung tính chất là khó hiểu và thử thách trí tuệ của con người.

Tam giác Penrose là một hình tam giác bất khả thi, vậy nên trong đời sống thực tế, nó không có nhiều ứng dụng. Tuy nhiên, tam giác Penrose được sử dụng trong nghệ thuật và thiết kế để tạo ra các hình ảnh và sản phẩm có tính thẩm mỹ cao và gây ấn tượng mạnh. Ngoài ra, đôi khi tam giác Penrose cũng được sử dụng trong lĩnh vực khoa học để giải các bài toán hình học tinh vi. Tuy nhiên, vì tam giác Penrose là một hình không thể tồn tại trong thực tế, nó không được áp dụng rộng rãi trong các lĩnh vực kỹ thuật hay sản xuất.

Tam giác Penrose liên quan rất nhiều đến nghệ thuật và thiết kế, và được coi là một trong những biểu tượng của hình học phi tuyến. Đây là một hình tam giác bất khả thi, được tạo ra bởi nhà toán học và nhà vật lý người Anh - Roger Penrose vào năm 1950. Tam giác Penrose được sử dụng rộng rãi trong nghệ thuật và thiết kế, đặc biệt là trong lĩnh vực quảng cáo và kiến trúc, để tạo ra những mẫu thiết kế độc đáo và gây ấn tượng mạnh cho người xem. Nó cũng thường được sử dụng như một biểu tượng của sự mâu thuẫn và sự phức tạp trong các tác phẩm nghệ thuật.

Xem thêm: Cách Đăng Ký Cuộc Gọi Nội Mạng Viettel 1 Tháng Ưu Đãi 2023, Đăng Ký Gọi Nội Mạng Viettel Giá Rẻ Nhất 2023

Tam giác Penrose là một hình học bất khả thi do nghệ sĩ Roger Penrose tạo ra vào năm 1958. Tam giác này được tạo thành bằng cách kết hợp ba cạnh đối xứng với nhau của một hình tam giác vuông đặc biệt. Cụ thể, tam giác Penrose được tạo thành bằng cách chia tỉ lệ tam giác vuông đặc biệt thành 3 phần, rồi sử dụng các phần đó để tạo thành các phần còn lại của tam giác. Các phần này được sắp xếp theo đúng thứ tự để tạo nên tam giác Penrose bất khả thi.Tam giác Penrose có cấu trúc đặc biệt vì nó không tuân theo các quy tắc hình học thông thường, không giống với tam giác đều hay các hình học khác. Thậm chí, khi nhìn tam giác Penrose từ một góc nhìn nào đó, nó có thể trông như một hình học khác hoàn toàn. Tuy nhiên, tam giác Penrose là một trong những hình học đặc biệt và phức tạp nhất được tạo ra cho đến nay và có thể được sử dụng để nghiên cứu các vấn đề liên quan đến toán học và khoa học tự nhiên.